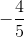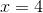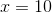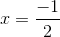All College Algebra Resources
Example Questions
Example Question #11 : Solving Exponential Functions
Solve for x:
In order to solve for x when it is in the exponent, we need to make the bases on either side of the equation look the same. In order to do this, divide both sides by the coefficient in order to get the exponent by itself. Then factor the larger number until it looks like the smaller one. For this problem that looks as follows:
Divide both sides by 5:
Factor the larger number:
Now substitute in the factored number:
Since the bases are now the same:
Example Question #41 : Exponential And Logarithmic Functions
Solve for x:
In order to solve for x when it is in the exponent, we need to make the bases on either side of the equation look the same. In order to do this, divide both sides by the coefficient in order to get the exponent by itself. Then factor the larger number until it looks like the smaller one. For this problem that looks as follows:
Divide both sides by 4:
Factor the larger number:
Now substitute in the factored number:
Since the bases are now the same:
Example Question #42 : Exponential And Logarithmic Functions
Solve the function:
Change the base of the right side to base two.
Rewrite the equation.
With similar bases, set the powers equal.
Solve for x.
Subtract 
Divide by negative five on both sides.
The answer is:
Example Question #43 : Exponential And Logarithmic Functions
Solve for x:
In order to solve for x when it is in the exponent, we need to make the bases on either side of the equation look the same. In order to do this, divide both sides by the coefficient in order to get the exponent by itself. Then factor the larger number until it looks like the smaller one. For this problem that looks as follows:
Divide both sides by 2:
Factor the larger number:
Now substitute in the factored number:
Since the bases are now the same:
Example Question #44 : Exponential And Logarithmic Functions
Solve:
Change the right side to base three.
With similar bases, the exponents can be set equal.
Subtract one from both sides.
The answer is:
Example Question #45 : Exponential And Logarithmic Functions
Solve:
None of these
add four to both sides:
divide both sides by four:
take the natural logarithm of both sides:
Divide both sides by three:
Example Question #46 : Exponential And Logarithmic Functions
Solve for x:
Step 1: We will take log of base 2 of both sides of the equation. The log base 2 will cancel out the base of the exponential term and just leave the exponent.
Step 2: We need to find the value of the right side. To find this number, we do the following:
Let 
Apply the rule: Raise the base of the log to the power (the solution), and this expression is equal to the value next to the base of the exponent.
So:
If 
So, 
Since the bases of the two exponential functions are the same, then the exponents of both exponential functions must also be the same.
The answer is:
Example Question #41 : Exponential And Logarithmic Functions
Solve for 
To solve for 
Example Question #42 : Exponential And Logarithmic Functions
Solve for 
Since the bases of the exponents are the same (4), the exponents have to equal each other for the exponential equation to be true.
Example Question #381 : Mathematical Relationships And Basic Graphs
Solve for 
To solve for 
Now, with the same base, the exponents can be set equal to each other:
Solving for 
All College Algebra Resources