All Calculus AB Resources
Example Questions
Example Question #51 : Integrating
Find 


When finding a function given the antiderivative, a good approach is to take the derivative of 
By using chain rule for the ln(4x)term, the derivative 1x is obtained. Power rule is used to differentiate the second term, and the last term, C, is simply a constant.
Therefore, the correct expression is f(x)=1x+3x2.
Example Question #52 : Integrating
Let 

For this problem, keep in mind that both terms (

Taking the derivative of 



Example Question #511 : Calculus Ab
Can the constant of integration (“C”) of an antiderivative be a negative value? Why is “C” important?
No; 
Yes; but the term is not relevant to the antiderivative
Yes; 
No; and the term is not relevant to the antiderivative
Yes; 
The constant of integration, also known as 
Essentially, part of the function can be isolated by taking the antiderivative, but the positioning of this function may differ depending on what constants should be present in the equation.
Because these constants could be either negative or positive, there are no restrictions on the exact sign of 

Example Question #54 : Integrating
Evaluate the following antiderivative:
Sometimes when there are multiple terms added or subtracted from one another within the antiderivative, it can be useful to invoke the following rule:
Separating the terms into two smaller antiderivative chunks can help declutter the problem at hand. Rewriting roots to look like exponents can also be useful.
The first chunk of this problem requires power rule, and the second is a trigonometry derivative identity. Finally, both 
Example Question #1 : Find Antiderivatives
Let 

This problem looks complicated at first, but it is really just a trigonometry derivative identity with an inner function of 
Since 
Example Question #512 : Calculus Ab
Let 

First, find the general expression of the antiderivative.
From here, the correct value of 

To finish this problem, we substitute 

Example Question #57 : Integrating
Evaluate the following antiderivative:
To simplify this problem, it may be useful to split up the integral into more manageable chunks:
Another trick is to rewrite roots to look like exponents (in this case,![\sqrt[4]{2x} \rightarrow (2x)^{\frac{1}{4}}](http://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1177374/gif.latex)
The 

Finally, multiply constants through to identify the correct answer:
Example Question #71 : Integrating
Use a change of variable (aka a u-substitution) to evaluate the integral,
Integrals such as this are seen very commonly in introductory calculus courses. It is often useful to look for patterns such as the fact that the polynomial under the radical in our example, 


Now differentiate with respect to 


Looking at equation (2), we can solve for 


Now proceed with the integration with respect to 

Now write the result in terms of 
Example Question #1 : Use Substitution And Integration
Use u-substitution to fine
Let
Then
Now we can substitute
Now we substitute back
Example Question #73 : Integrating
Evaluate
We can use substitution for this integral.
Let 
then 
Multiplying this last equation by 

Now we can make our substitutions













All Calculus AB Resources





![f(x)=\frac{d}{dx} F(x) =\frac{d}{dx} [ln|4x|+x^3+C]=\frac{1}{x}+3x^2+0=\frac{1}{x}+3x^2](http://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1177278/gif.latex)







![F(x)=\int \sqrt[3]{2x}+sec(x)tan(x) dx](http://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1177366/gif.latex)




![F(x)=\int \sqrt[3]{2x}+sec(x)tan(x) dx](http://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1177367/gif.latex)
![F(x)=\int \sqrt[3]{2x} dx + \int sec(x)tan(x) dx](http://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1177368/gif.latex)
![F(x) =\int (2x)^{\frac{1}{3}} dx + sec(x)tan(x) dx=[(\frac{1}{2})(\frac{3}{4})(2x)^{\frac{4}{3}}+C_1] + [sec(x)+C_2]](http://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1177369/gif.latex)






![F(x)=\int f(x) dx = \int csc(2x+7)cot(2x+7) dx = (\frac{1}{2})[-csc(2x+7)]+C](http://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1177349/gif.latex)














![F(x)=\int 5(x^7-8x+2)-\sqrt[4]{2x} dx](http://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1177372/gif.latex)




![F(x)=\int 5(x^7-8x+2)-\sqrt[4]{2x} dx=\int 5(x^7-8x+2) dx-\int \sqrt[4]{2x} dx](http://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1177373/gif.latex)

![5[(\frac{1}{8})x^8-(\frac{1}{2})(8x^2)+2x]+C1 - (\frac{4}{5})(\frac{1}{2})(2x)^{\frac{5}{4}}+C_2](http://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1177376/gif.latex)





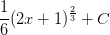
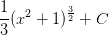


![= \frac{1}{2}\left[\frac{1}{\frac{1}{2}+1}u^{\frac{1}{2}+1} \right ]+C](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/741662/gif.latex)
























