All Calculus AB Resources
Example Questions
Example Question #21 : Integrating
Using the Fundamental Theorem of Calculus solve the integral.
To solve the integral using the Fundamental Theorem, we must first take the anti-derivative of the function. The anti-derivative of 


When we do this,


The next step is to find the difference between the values at each limit of integration, because the Fundamental Theorem states

Thus, we subtract 

Example Question #35 : Integrating
Solve 
To solve the integral, we first have to know that the fundamental theorem of calculus is

Since 
The anti-derivative of the function 


When we plug 3 into the anti-derivative, the solution is 
To find the final answer, we must take the difference of these two solutions, so the final answer is 
Example Question #21 : Integrating
Solve 
To solve the integral, we first have to know that the fundamental theorem of calculus is

Since 
The anti-derivative of the function

is

so we must evaluate 
When we plug 3 into the anti-derivative, the solution is 
To find the final answer, we must take the difference of these two solutions, so the final answer is 
Example Question #22 : Integrating
Evaluate the indefinite integral:
First, compute the indefinite integral:
Note that the 

Now the integral can be written in terms of
Therefore:
When we go to compute the indefinite integral the constant of integration 
We can precede by either going back to the original variable 

Solution 1)



Solution 2)
We could have also solved without converting back to the original variable. Instead, we could just change the limits of integration. Use the definition assigned to the variable 




Example Question #38 : Integrating
This is a Fundamental Theorem of Calculus problem. Since a derivative and anti-derivative cancel each other out, we simply have to plug the limits into our function (with the outside variable). Then, we multiply each by the derivative of the bound:
Example Question #23 : Integrating
Using the Fundamental Theorem of Calculus, the derivative of an anti-derivative simply gives us the function with the limits plugged in multiplied by the derivative of the respective bounds:
In the last step, we made use of the following trigonometric identity:
Example Question #24 : Integrating
Evaluate the following indefinite integral:
Evaluate the following indefinite integral:
Recall that we can split subtraction and addition within integrals into separate integrals. This means that we can look at our problem in two steps.
Recall that we can integrate any exponential term by adding 1 to the exponent and dividing by the new exponent.
So,
Next, recall that the integral of sine is negative cosine. However, we already have a negative sine, so we should get positive cosine.
Now, we can combine our two halves to get our final answer.
Notice that we only have one "c" because c is just a constant, not a variable.
Example Question #491 : Calculus Ab
If 
Remember that the notation for the antiderivative may appear as 
Conceptually, it might be useful to think of the antiderivative as the “opposite” of the derivative function. Essentially, the antiderivative “undoes” the derivative.
However, since taking the derivative of a constant results in zero, any constants not accounted for by the antiderivative must be represented by the variable 
The expression that contains all the correct components of the antiderivative expression (including 



Example Question #492 : Calculus Ab
Find the antiderivative of the function 
To check our work, let’s take the derivative of our answer. This is a useful strategy to determine if the antiderivative was found correctly, since
Note that there are two functions present (

We obtain the original function, 





Example Question #493 : Calculus Ab
Let 

To approach this problem, first find the general antiderivative expression for the function 
Then, the goal is to find the correct value of 

The value of Cis solved for by plugging in 


All Calculus AB Resources












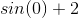



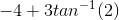












![\int_0^{\frac{\pi}{4}}\tan(x)\sec^2(x)dx=\left[ \frac{1}{2}\tan^2(x)\right ]_{x=0}^{x=\frac{\pi}{4}}\: \: =\: \: \: \: \frac{1}{2}\tan^2\left(\frac{\pi}{4}\right) -\frac{1}{2}\tan^2\left(0\right)](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/933356/gif.latex)



![\int_0^1 udu =\left[\frac{1}{2}u^2 \right ]_{u=0}^{u=1} =\frac{1}{2}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/926667/gif.latex)




































![\frac{d}{dx} [2sin(2t)+C]=2cos(2t)(2)+0=4cos(2t)](http://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1177302/gif.latex)










