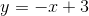This is a related rates problem.

Since the problem gives the time for one orbit, we can find the angular speed of the point. The angular speed is simply how many radians the particle travels in one second. We find this by dividing the number of radians in one revolution, , by the time it takes to travel one revolution, 8 seconds.

This gives us the change in the angle with respect to time, .

Now we need to relate the  position to the angle, . Recall that

, where r is the radius.

Since the radius is given as 1 unit, we can write this equation as

.

Now we take the derivative of both sides with respect to time, using implicit differentiation. Remember that we use the chain rule for any variable that is not . This gives,

.

Now we have a formula that relates the horizontal speed of the particle at an instant in time, , to the angle above the positive x-axis and angular speed at that same instant. We are told to find how fast the x coordinate is changing when the angle,  is  radians above the positive x-axis. So we will plug in  for . However, we also need to know . Fortunately, we already found it. It is the angular speed,  radians/second.

Plugging this information in, we get

This is the answer. The negative makes sense because the point is traveling counter-clockwise. Hence, it is moving left when the angle is  radians.

This is a related rates problem. The ladder leaning against the side of a building forms a right triangle, with the 10ft ladder as its hypotenuse. The Pythagorean Theorem,  relates all three sides of this triangle to each other. Let  be the height from the top of the ladder to the ground. Let  be the distance from the bottom of the ladder to the building. Since 10 is the hypotenuse, we have the following equation.

Simplifying the right side gives us

Since  and  are variables, we will wait to plug values into them until after we take the derivative.

The question asks how fast the man standing on the top of the ladder is falling whenthe ladder's base is 6ft from the building and is sliding away at 2 ft/sec. These two values,  and , only happen at a single instant in time. So we will find the derivative of the equation at this point in time.

Using implicit differentiation to find the derivative with respect to time, we get

We only care about the instant that  and . We need to find the rate that the top of the ladder, and thus the man, is falling. So we want to solve for . However, we will need to know what  is at this instant in order to find an answer. Fortunately, the Pythagorean Theorem applies at all points in time, so we can use it for this particular instant to find .

Since we are dealing with physical distances, we will only use the positive 8.

Plugging all the information into our derivative equation gives us

The negative makes sense because the man is falling down, so the height is getting smaller. Thus our answer is 

To find the total distance traveled, the velocity function has to be integrated from  to  hours:

Finally, the question is asking how far the car will be from home.  It was 3 miles from home when , so at , it will be:

 miles from home.

Differentiate, 

Strategy 

This one at first glance appears difficult even if we recognize that the chain rule is needed; we have a function within a function within a function within a function. To avoid making mistakes, it's best to start by defining variables to make the calculation easier to follow. 

Let's start with the outermost function, we will write  as a function of  by setting, 

______________________________________________________ 

_______________________________________________________

Similarly, define  to write  as a function of  

_______________________________________________________

Write  as a function of 

_______________________________________________________

Finally, define the inner-most function, , as the function of 

 ________________________________________________________

Since  we will just substitute that in and move to the front. 

That was easy enough, now just write everything in terms of  by going back to the definitions of   and .

To find the tangent line at the given point, we need to first take the derivative of the given function. 

Power Rule:

The Power Rule says that we take the exponent of the “x” value and bring it to the front. Then we subtract one from the exponent.

Therefore,  becomes 

From there we plug in the "1" from the point to get our m value of the equation . When we plug in "1" to y' we get m=-1. Then from there, we will plug our point into  now that we have found m to find our b value. So,

Therefore, the tangent line is equal to

To find the tangent line at the given point, we need to first take the derivative of the given function. The rule for functions with "e" in it says that the derivative of  However with this function there is also a 3 in the exponent so we will also use chain rule. Chain Rules states that we work from the outside to the inside. Meaning we will take the derivative of the outside of the equation and multiply it by the derivative of the inside of the equation.

To put this into equation it will look like 

From there we plug in the "0" from the point to get our m value of the equation . When we plug in "0" to y' we get m=3. Then from there, we will plug our point into   now that we have found m to find our m value. So,

 then plug this all back into the equation once more and we are left with

To find the tangent line at the given point, we need to first take the derivative of the given function using Power Rule

Power rule says that we take the exponent of the “x” value and bring it to the front. Then we subtract one from the exponent. 

From there we plug in the "2" from the point to get our m value of the equation. When we plug in "2" to y' we get m=8. Then from there, we will plug our point into now that we have found m to find our b value. So,

Plug this back into 

Find the equation of the line tangent to the curve  at the given point

The slope of the line tangent at the given point will be equal to the derivative of  at that point. Compute the derivative and find the slope for our line: 

Evaluate the secant term: 

Therefore slope of the tangent line is simply: 

So now we know the slope of the tangent line and can write the equation then solve for  

In order to solve for  we need one point on the line. Use the point where the tangent line meets the curve. Use the original function to find the "y" coordinate at this point: 

We now have our point:

Use the point to find 

Find the slope of the line tangent to the curve of d(g) when g=6.

All we need here is the power rule. This states that to find the derivative of a polynomial, simply subtract 1 from each exponent and then multiply each term by their original exponent. 

Constant terms will drop out when we do this, and linear terms will become constants.

From here substitute in g=6.

The tangent line to the graph of  at point  is the line with slope  that passes through that point. Find the derivative :

Apply the sum rule:

The tangent line is therefore the line with slope 5 through . Apply the point-slope formula: