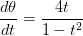Call Now to Set Up Tutoring:

(888) 888-0446

Calculus AB : Calculus AB

Study concepts, example questions & explanations for Calculus AB

Create An Account

All Calculus AB Resources

45 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Calculate Position, Velocity, And Acceleration

A particle's position on the -axis is given by the function $f(t)=\sin(t)-t+1$ from $0 < t <\pi$ .

When does the particle change direction?

Possible Answers:

$x=2\pi$

$x= \frac{\pi}{4}$

$x= \pi$

$x=\frac{\pi}{2}$

It doesn't change direction within the given bounds

Correct answer:

It doesn't change direction within the given bounds

Explanation:

To find when the particle changes direction, we need to find the critical values of f(t) . This is done by finding the velocity function, setting it equal to , and solving for

$0=v(t) = f'(t) = \cos(t)-1$ .

Hence $\cos(t)=1$ .

The solutions to this on the unit circle are $t =0, \pi$ , so these are the values of where the particle would normally change direction. However, our given interval is $0 < t < \pi$ , which does not contain $0, \pi$ . Hence the particle does not change direction on the given interval.

Report an Error

Example Question #4 : Calculate Position, Velocity, And Acceleration

A particle moves in space with velocity given by

$v(t)=\alpha t^3+\beta \sqrt{t}$

where $\alpha, \beta$ are constant parameters.

Find the acceleration of the particle when t=4 .

Possible Answers:

$48\alpha +2\beta$

$3\alpha t^2+\frac{\beta}{2\sqrt{t}}$

$48\alpha + \frac{\beta}{4}$

Correct answer:

$48\alpha + \frac{\beta}{4}$

Explanation:

To find the acceleration of the particle, we must take the first derivative of the velocity function:

$a(t)=v'(t)=3\alpha t^2+\frac{\beta}{2\sqrt{t}}$

The derivative was found using the following rule:

$\frac{\mathrm{d} }{\mathrm{d} x} x^n=nx^{n-1}$

Now, we evaluate the acceleration function at the given point:

$a(4)=3\alpha(4^2)+\frac{\beta}{2\sqrt{4}}=48\alpha+\frac{\beta}{4}$

Report an Error

Example Question #21 : Contextual Applications Of Derivatives

Find the velocity function from an acceleration function given by

a(t)=4t+5

and the condition v(0)=10

Possible Answers:

2t^2+5t+C

2t^2+5t

2t^2+15

2t^2+5t+10

Correct answer:

2t^2+5t+10

Explanation:

Acceleration is the rate of change of velocity, so we must integrate the acceleration function to find the velocity function:

$v(t)=\int a(t)dt=\int (4t+5 ) dt=2t^2+5t+C$

The integration was performed using the following rules:

$\int x^ndx=\frac{x^{n+1}}{n+1}+C$ , $\int a dx=ax+C$

To find the integration constant C, we must use the initial condition given:

v(0)=10=2(0)^2+5(0)+C

C=10

Our final answer is

v(t)=2t^2+5t+10

Report an Error

Example Question #321 : Calculus Ab

The velocity of a particle is given by v(t). Find the function which models the particle's acceleration.

v(t)=3t^3-4t^2-5t+16

Possible Answers:

a(t)=9t^2-8t-5

a(t)=9t^3+8t^2-5

a(t)=9t^2-8t-17

a(t)=6t^2-8t+5

Correct answer:

a(t)=9t^2-8t-5

Explanation:

The velocity of a particle is given by v(t). Find the function which models the particle's acceleration.

v(t)=3t^3-4t^2-5t+16

To find the acceleration from a velocity function, simply take the derivative.

In this case, we are given v(t), and we need to find v'(t) because v'(t)=a(t).

To find v'(t), we need to use the power rule.

For each term, simply multiply by the exponent, and then subtract one from the exponent. Constant terms will drop out, linear terms will become constants, and so on.

v(t)=3t^3-4t^2-5t+16

$v'(t)=a(t)=(3)3t^{3-1}-(2)4t^{2-1}-5=9t^2-8t-5$

So, our answer is:

a(t)=9t^2-8t-5

Report an Error

Example Question #11 : Calculate Position, Velocity, And Acceleration

The velocity of a particle is given by v(t) . Find the particle's acceleration when t=3 .

v(t)=3t^3-4t^2-5t+16

Possible Answers:

a=53

a=27

a=-3

a=52

Correct answer:

a=52

Explanation:

The velocity of a particle is given by v(t) . Find the particle's acceleration when t=3 .

v(t)=3t^3-4t^2-5t+16

To find the acceleration from a velocity function, simply take the derivative.

In this case, we are given v(t) , and we need to find v'(t) because v'(t)=a(t) .

To find v'(t) , we need to use the power rule.

For each term, simply multiply by the exponent, and then subtract one from the exponent. Constant terms will drop out, linear terms will become constants, and so on.

v(t)=3t^3-4t^2-5t+16

$v'(t)=a(t)=(3)3t^{3-1}-(2)4t^{2-1}-5=9t^2-8t-5$

So, our acceleration function is:

a(t)=9t^2-8t-5

Now, plug in for and solve.

a(3)=9(3)^2-8(3)-5=81-24-5=52

So, our answer is .

Report an Error

Example Question #1 : Calculate Rates Of Change And Related Rates

A right triangle has sides of length and which are both increasing in length over time such that:

x(t)=2t

y(t)=4t^2

a) Find the rate at which the angle $\theta$ opposite y(t) is changing with respect to time.

Possible Answers:

$\frac{d\theta}{dt}=\frac{4t}{1-t^2}$

$\frac{d\theta}{dt}=\cos(t)-\frac{1}{1+t}$

$\frac{d\theta}{dt}=t+\frac{4}{1+2t^2}$

$\frac{d\theta}{dt}=\sin(t)+\frac{1}{1+t}$

$\frac{d\theta}{dt}=\frac{2}{1+4t^2}$

Correct answer:

$\frac{d\theta}{dt}=\frac{2}{1+4t^2}$

Explanation:

A right triangle has sides of lenght and which are both increasing in length over time such that:

x(t)=2t

y(t)=4t^2

Find the rate at which the angle $\theta$ opposite y(t) is changing with respect to time.

Screen shot 2020 09 04 at 11.29.59 am

a) First, we need to write an expression for the angle $\theta$ as a function of . Because the angle is opposite the side we know that the tangent is simply y/x . Take the inverse of the tangent:

$\theta (t)\, \, =\, \, \tan^{-1}\left(\frac{y(t)}{x(t)} \right )\: \: =\: \: \tan^{-1}\left(\frac{4t^2}{2t}\right)\, \, =\, \, \tan^{-1}\left(2t \right )$

$\theta(t)=\tan^{-1}(2t)$

Now we need to differentiate with respect to .

Recall the general derivative for the inverse tangent function is:

$\frac{d}{dx}\tan^{-1}(x)=\frac{1}{1+x^2}$

Applying this to our function for $\theta(t)$ , and remembering to use the chain rule, we obtain:

$\frac{d\theta}{dt}=\frac{d}{dt}\tan^{-1}(2t)=\frac{2}{1+(2t)^2}=\frac{2}{1+4t^2}$

$\frac{d\theta}{dt}=\frac{2}{1+4t^2}$

Report an Error

Example Question #2 : Calculate Rates Of Change And Related Rates

Soap is sometimes used to determine the location of leaks in industrial pipes. A perfectly spherical soap bubble is growing at a rate of 5 mm^3/sec . What is the rate of change of the surface area of the bubble when the radius of the bubble is 10 mm ?

Possible Answers:

$\frac{1}{80\pi} mm^2/sec$

1 mm^2/sec

80 mm^2/sec

$80\pi mm^2/sec$

Correct answer:

1 mm^2/sec

Explanation:

To determine the rate of change of the surface area of the spherical bubble, we must relate it to something we do know the rate of change of - the volume.

The volume of a sphere is given by the following:

$V=\frac{4\pi}{3}r^3$

The rate of change of the volume is given by the derivative with respect to time:

$\frac{\mathrm{d} V}{\mathrm{d} t}=4\pi r^2 \frac{\mathrm{d} r}{\mathrm{d} t}$

The derivative was found using the following rules:

$\frac{\mathrm{d} }{\mathrm{d} x} f(g(x))=f'(g(x)) \cdot g'(x)$ , $\frac{\mathrm{d} }{\mathrm{d} x}x^n=nx^{n-1}$

We must now solve for the rate of change of the radius at the specified radius, so that we can later solve for the rate of change of surface area:

$5=4\pi (100) \frac{\mathrm{d} r}{\mathrm{d} t}$

$\frac{\mathrm{d} r}{\mathrm{d} t}=\frac{1}{80\pi}$

Next, we must find the surface area and rate of change of the surface area of the sphere the same way as above:

$A=4\pi r^2$

$\frac{\mathrm{d} A}{\mathrm{d} t}=8 \pi r \frac{\mathrm{d} r}{\mathrm{d} t}$

Plugging in the known rate of change of the surface area at the specified radius, and this radius into the rate of surface area change function, we get

$\frac{\mathrm{d} A}{\mathrm{d} t}=8\pi (10)\cdot \frac{1}{80\pi}= 1mm^2/sec$

Report an Error

Example Question #1 : Calculate Rates Of Change And Related Rates

A pizzeria chef is flattening a circular piece of dough. The surface area of the dough (we are only considering the top of the dough) is increasing at a rate of 0.5 inches/sec. How quickly is the diameter of the pizza changing when the radius of the pizza measures 4 inches?

Possible Answers:

inches/sec

$\frac{1}{16 \pi}$ inches/sec

inches/sec

$\frac{1}{8 \pi}$ inches/sec

Correct answer:

$\frac{1}{8 \pi}$ inches/sec

Explanation:

To find the rate of change of the diameter, we must relate the diameter to something we do know the rate of change of: the surface area.

The surface area of the top side of the pizza dough is given by

$A=\pi r ^2$

The rate of change, then, is found by taking the derivative of the function with respect to time:

$\frac{\mathrm{d} A}{\mathrm{d} t}=2\pi r \frac{\mathrm{d} r}{\mathrm{d} t}$

Solving for the rate of change of the radius at the given radius, we get

$\frac{1}{2}=2\pi (4)\frac{\mathrm{d} r}{\mathrm{d} t}$

$\frac{\mathrm{d} r}{\mathrm{d} t}=\frac{1}{16\pi}$ inches/sec

Now, we relate the diameter to the radius of the pizza dough:

2r=d

Taking the derivative of both sides with respect to time, we get

$2 \frac{\mathrm{d} r}{\mathrm{d} t}=\frac{\mathrm{d} d}{\mathrm{d} t}$

Plugging in the known rate of change of the radius at the given radius, we get

$\frac{\mathrm{d} d}{\mathrm{d} t}=\frac{1}{8\pi}$ inches/sec

We could have found this directly by writing our surface area formula in terms of diameter, however the process we used is more applicable to problems in which the related rate of change is of something not as easy to manipulate.

Report an Error

Example Question #2 : Calculate Rates Of Change And Related Rates

A spherical balloon is increasing in volume at a constant rate of 0.1 cm^3/min . At a radius of 3 cm, what is the rate of change of the circumference of the balloon?

Possible Answers:

$\frac{1}{90\pi} cm/min$

$\frac{1}{180} cm/min$

$\frac{1}{90} cm/min$

$\frac{1}{360} cm/min$

$\frac{1}{360\pi} cm/min$

Correct answer:

$\frac{1}{180} cm/min$

Explanation:

To determine the rate of change of the circumference at a given radius, we must relate the circumference rate of change to the rate of change we know - that of the volume.

Starting with the equation for the volume of the spherical balloon,

$V=\frac{4}{3}\pi r^3$

we take the derivative of the function with respect to time, giving us the rate of change of the volume:

$\frac{\mathrm{d} V}{\mathrm{d} t}=4\pi r^2 \frac{\mathrm{d} r}{\mathrm{d} t}$

The derivative was found using the following rules:

$\frac{\mathrm{d} }{\mathrm{d} x} x^n=nx^{n-1}$ , $\frac{\mathrm{d} }{\mathrm{d} x} f(g(x))=f'(g(x))\cdot g'(x)$

The chain rule was used when taking the derivative of the radius with respect to time, because we know that it is a function of time.

Solving for $\frac{\mathrm{d} r}{\mathrm{d} t}$ using our known $\frac{\mathrm{d} V}{\mathrm{d} t}$ at the given radius, we get

$\frac{\mathrm{d} r}{\mathrm{d} t}=\frac{1}{360\pi} cm/min$

Now, we use this rate of change and apply it to the rate of change of the circumference, which we get by taking the derivative of the circumference with respect to time:

$c=2\pi r$

$\frac{\mathrm{d} c}{\mathrm{d} t}=2\pi \frac{\mathrm{d} r}{\mathrm{d} t}$

Solving for the rate of change of the circumference by plugging in the known rate of change of the radius, we get

$\frac{\mathrm{d} c}{\mathrm{d} t}=2\pi (\frac{1}{360 \pi})=\frac{1}{180} cm/min$

Report an Error

Example Question #3 : Calculate Rates Of Change And Related Rates

Determine the rate of change of the angle opposite the base of a right triangle -whose length is increasing at a rate of 1 inch per minute, and whose height is a constant 2 inches - when the area of the triangle is 2 square inches.

Possible Answers:

$\frac{1}{4}$ radians per minute

$\frac{1}{\sqrt{2}}$ radians per minute

$\frac{1}{4\sqrt{2}}$ radians per minute

$\frac{1}{2\sqrt{2}}$ radians per minute

Correct answer:

$\frac{1}{\sqrt{2}}$ radians per minute

Explanation:

To determine the rate of the change of the angle opposite to the base of the given right triangle, we must relate it to the rate of change of the base of the triangle when the triangle is a certain area.

First, we must determine the length of the base of the right triangle at the given area:

$A=\frac{bh}{2}$

4=b(2)

b=2

Now, we must find something that relates the angle opposite of the base to the length of the base and height - the tangent of the angle:

$\tan \theta=\frac{b}{h}$

To find the rate of change of the angle, we take the derivative of both sides with respect to time, keeping in mind that the base of the triangle is dependent on time, while the height is constant:

$\sec^2(\theta)\frac{\mathrm{d} \theta}{\mathrm{d} t}=\frac{2}{2}\frac{\mathrm{d} b}{\mathrm{d} t}$

We know the rate of change of the base, and we can find the angle from the sides of the triangle:

$\tan(\theta)=1$

$\theta=\frac{\pi}{4}$

Plugging this and the other known information in and solving for the rate of change of the angle adjacent to the base, we get

$\sec^2(\frac{\pi}{4})\frac{\mathrm{d} \theta}{\mathrm{d} t}=1$

$\frac{\mathrm{d} \theta}{\mathrm{d} t}=\frac{1}{\sqrt{2}}$ radians per minute

Report an Error

View Tutors

Joshua
Certified Tutor

Cedarville University, Bachelor in Arts, International and Comparative Education.

View Tutors

Jessica
Certified Tutor

Grand Rapids Community College, Associate in Science, Psychology.

View Tutors

Adriana
Certified Tutor

CUNY Hunter College, Bachelor in Arts, Mathematics. University of Connecticut, Master of Science, Mathematics.

All Calculus AB Resources

45 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Biology Tutors in San Francisco-Bay Area, Spanish Tutors in San Francisco-Bay Area, Calculus Tutors in Los Angeles, LSAT Tutors in New York City, Spanish Tutors in Washington DC, Chemistry Tutors in Denver, Calculus Tutors in Denver, MCAT Tutors in Philadelphia, Chemistry Tutors in Los Angeles, Statistics Tutors in Miami

Popular Courses & Classes

ACT Courses & Classes in Atlanta, GRE Courses & Classes in New York City, GRE Courses & Classes in Dallas Fort Worth, SAT Courses & Classes in San Diego, MCAT Courses & Classes in Phoenix, SAT Courses & Classes in Miami, SAT Courses & Classes in Phoenix, ACT Courses & Classes in Chicago, LSAT Courses & Classes in Los Angeles, ACT Courses & Classes in Philadelphia

Popular Test Prep

GMAT Test Prep in San Francisco-Bay Area, SSAT Test Prep in New York City, GMAT Test Prep in Seattle, ACT Test Prep in Atlanta, ISEE Test Prep in Boston, SSAT Test Prep in Phoenix, SSAT Test Prep in Miami, GRE Test Prep in Seattle, GMAT Test Prep in San Diego, SSAT Test Prep in Chicago

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Calculus AB : Calculus AB

Study concepts, example questions & explanations for Calculus AB

All Calculus AB Resources

Example Questions

Example Question #1 : Calculate Position, Velocity, And Acceleration

Example Question #4 : Calculate Position, Velocity, And Acceleration

Example Question #21 : Contextual Applications Of Derivatives

Example Question #321 : Calculus Ab

Example Question #11 : Calculate Position, Velocity, And Acceleration

Example Question #1 : Calculate Rates Of Change And Related Rates

Example Question #2 : Calculate Rates Of Change And Related Rates

Example Question #1 : Calculate Rates Of Change And Related Rates

Example Question #2 : Calculate Rates Of Change And Related Rates

Example Question #3 : Calculate Rates Of Change And Related Rates

All Calculus AB Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: