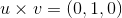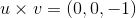We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

Calculus 3 : Vectors and Vector Operations

Study concepts, example questions & explanations for Calculus 3

Create An Account

All Calculus 3 Resources

6 Diagnostic Tests 373 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Parametric Curves

Find the length of the parametric curve described by

$x = 2\sin t$

$y = 2\cos t$

from t=0 to $\pi$ .

Possible Answers:

None of the other answers

$\pi$

$4\pi$

$\frac{3\pi}{4}$

$2\pi$

Correct answer:

$2\pi$

Explanation:

There are several ways to solve this problem, but the most effective would be to notice that we can derive the following-

$x^2 = 4\sin^2t$

$y^2 = 4\cos^2t$

Hence

$x^2+y^2 = 4\sin^2t + 4\cos^2t = 4$

Therefore our curve is a circle of radius $\sqrt4=2$ , and it's circumfrence is $4\pi$ . But we are only interested in half that circumfrence ( is from to $\pi$ , not $2\pi$ .), so our answer is $2\pi$ .

Alternatively, we could've found the length using the formula

$l = \int_{t_0}^{t_1}\sqrt{(\frac{dx}{dt})^2+(\frac{dy}{dt})^2}dt$ .

Report an Error

Example Question #2 : Parametric Curves

Find the coordinates of the curve function

c(t)=<t^2,t,-3t>
when t=5 .

Possible Answers:

c(5)=<30,10,-5>

c(5)=<25,5,-15>

c(5)=<2,4,6>

c(5)=<15,10,-10>

Correct answer:

c(5)=<25,5,-15>

Explanation:

To find the coordinates, we set t=5 into the curve function.

We get

c(5)=<5^2,5,-3(5)>

and thus

c(5)=<25,5,-15>

Report an Error

Example Question #1 : Parametric Curves

Find the coordinates of the curve function

c(t)=<5,t^2,t>

when t=3

Possible Answers:

<-5,6,3>

<0,0,3>

<5,9,3>

<0,3,0>

Correct answer:

<5,9,3>

Explanation:

To find the coordinates, we evaluate the curve function for t=3

As such,

c(3)=<5, 3^2, 3)>=<5,9,3>

Report an Error

Example Question #4 : Parametric Curves

Find the coordinates of the curve function

c(t)=<cos (t), sin (t), cos (t)>

when $t=\frac{\pi}{2}$

Possible Answers:

<0,1,0>

<1,0,1>

<1,1,1>

$<\frac{1}{2},-\frac{1}{2},\frac{1}{2}>$

Correct answer:

<0,1,0>

Explanation:

To find the coordinates, we evaluate the curve function for $t=\pi/2$

As such,

$c(\frac{\pi}{2})=<cos (\frac{\pi}{2}), sin (\frac{\pi}{2}), cos (\frac{\pi}{2})>=<0,1,0>$

Report an Error

Example Question #5 : Parametric Curves

Find the equation of the line passing through the two points, given in parametric form:

(1, 2, 3), (0, -4, 1)

Possible Answers:

$\left \langle 1-t, 2+6t, 3+2t\right \rangle$

$\left \langle 1+t, 2+6t, 3+2t\right \rangle$

$\left \langle 1+t, 2-6t, 3+2t\right \rangle$

$\left \langle 1+t, 2+t, 3+t\right \rangle$

Correct answer:

$\left \langle 1+t, 2+6t, 3+2t\right \rangle$

Explanation:

To find the equation of the line passing through these two points, we must first find the vector between them:

$\vec{v}=\left \langle 1, 6, 2\right \rangle$

This was done by finding the difference between the x, y, and z components for the vectors. (This can be done in either order, it doesn't matter.)

Now, pick a point to be used in the equation of the line, as the initial point. We write the equation of line as follows:

$\vec{r}=\left \langle 1, 2, 3\right \rangle + t\left \langle 1, 6, 2\right \rangle=\left \langle 1+t, 2+6t, 3+2t\right \rangle$

The choice of initial point is arbitrary.

Report an Error

Example Question #4 : Parametric Curves

Find the coordinate of the parametric curve when

$t=\pi/2$

$x=sin\,t$ , y=t^2

Possible Answers:

$(1/2, \pi/6)$

$(0,\pi/2)$

$(1,\pi^2/4)$

Correct answer:

$(1,\pi^2/4)$

Explanation:

To find the coordinates of the parametric curve we plug in for

$t=\pi/2$ .

$x=sin\,(\pi/2)= 1$

$y=(\pi/2)^2=\pi^2/4$

As such the coordinates are

$(1,\pi^2/4)$

Report an Error

Example Question #1 : Cross Product

Let u=(2,4,5) , and v=(-2,6,10) .

Find $u\times v$ .

Possible Answers:

$u\times v=(10,-30,20)$

$u\times v=(0,-3,2)$

$u\times v=(40,-20,12)$

$u\times v=(-10,30,-20)$

$u\times v=(10,30,20)$

Correct answer:

$u\times v=(10,-30,20)$

Explanation:

We are trying to find the cross product between and .

Recall the formula for cross product.

If u=(u_x,u_y,u_z) , and v=(v_x,v_y,v_z) , then

$u\times v=(u_yv_z-u_zv_y, -u_xv_z+u_zv_x, u_xv_y-u_yv_x)$ .

Now apply this to our situation.

$u\times v=(4(10)-5(6),-2(10)+5(-2), 2(6)-4(-2))$

$u\times v=(40-30,-20-10, 12+8)$

$u\times v=(10,-30,20)$

Report an Error

Example Question #1 : Cross Product

Let u=(1,0,1) , and v=(0,0,1) .

Find $u\times v$ .

Possible Answers:

$u\times v=(0,0,-1)$

$u\times v=(-1,0,0)$

$u\times v=(0,0,0)$

$u\times v=(0,-1,0)$

$u\times v=(0,1,0)$

Correct answer:

$u\times v=(0,-1,0)$

Explanation:

We are trying to find the cross product between and .

Recall the formula for cross product.

If u=(u_x,u_y,u_z) , and v=(v_x,v_y,v_z) , then

$u\times v=(u_yv_z-u_zv_y, -u_xv_z+u_zv_x, u_xv_y-u_yv_x)$ .

Now apply this to our situation.

$u\times v=(0(1)-1(0),-1(1)+1(0), 1(0)-0(0))$

$u\times v=(0-0,-1+0, 0-0)$

$u\times v=(0,-1,0)$

Report an Error

Example Question #3 : Cross Product

True or False: The cross product can only be taken of two 3-dimensional vectors.

Possible Answers:

False

True

Correct answer:

True

Explanation:

This is true. The cross product is defined this way. The dot product however can be taken for two vectors of dimension n (provided that both vectors are the same dimension).

Report an Error

Example Question #4 : Cross Product

Which of the following choices is true?

Possible Answers:

$\begin{matrix}\vec{A}\cdot \vec{B}=-\vec{B}\cdot \vec{A}, & & \vec{A} \times \vec{B}= \vec{B}\times \vec{A} \end{matrix}$

$\begin{matrix}\vec{A}\cdot \vec{B}=\vec{B}\cdot \vec{A}, & & \vec{A} \times \vec{B}= - \vec{B}\times \vec{A} \end{matrix}$

$\begin{matrix}\vec{A}\cdot \vec{B}=\vec{B}\cdot \vec{A}, & & \vec{A} \times \vec{B}= \vec{B}\times \vec{A} \end{matrix}$

$\begin{matrix}\vec{A}\cdot \vec{B}=-\vec{B}\cdot \vec{A}, & & \vec{A} \times \vec{B}= - \vec{B}\times \vec{A} \end{matrix}$

Correct answer:

$\begin{matrix}\vec{A}\cdot \vec{B}=\vec{B}\cdot \vec{A}, & & \vec{A} \times \vec{B}= - \vec{B}\times \vec{A} \end{matrix}$

Explanation:

By definition, the order of the dot product of two vectors does not matter, as the final output is a scalar. However, the cross product of two vectors will change signs depending on the order that they are crossed. Therefore

$\begin{matrix}\vec{A}\cdot \vec{B}=\vec{B}\cdot \vec{A}, & & \vec{A} \times \vec{B}= - \vec{B}\times \vec{A} \end{matrix}$ .

Report an Error

View Calculus 3 Tutors

Dalton
Certified Tutor

University of Massachusetts Amherst, Doctor of Philosophy, Mathematics.

View Calculus 3 Tutors

Fathima
Certified Tutor

BITS Pilani Goa, Doctorate (PhD), Mathematics.

View Calculus 3 Tutors

Wysheka
Certified Tutor

Clemson University, Doctorate (PhD), Engineering and Science Education.

All Calculus 3 Resources

6 Diagnostic Tests 373 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

GRE Tutors in Miami, Biology Tutors in Philadelphia, SSAT Tutors in Dallas Fort Worth, Physics Tutors in Washington DC, SAT Tutors in Seattle, ACT Tutors in New York City, English Tutors in Phoenix, SAT Tutors in Atlanta, MCAT Tutors in Denver, Biology Tutors in Boston

Popular Courses & Classes

LSAT Courses & Classes in San Francisco-Bay Area, GRE Courses & Classes in Phoenix, GRE Courses & Classes in Boston, GRE Courses & Classes in Washington DC, GRE Courses & Classes in Los Angeles, Spanish Courses & Classes in Houston, Spanish Courses & Classes in Atlanta, SAT Courses & Classes in Atlanta, GRE Courses & Classes in Dallas Fort Worth, ISEE Courses & Classes in San Francisco-Bay Area

Popular Test Prep

SAT Test Prep in Houston, GRE Test Prep in Dallas Fort Worth, MCAT Test Prep in Boston, ISEE Test Prep in Houston, LSAT Test Prep in San Francisco-Bay Area, LSAT Test Prep in Seattle, SSAT Test Prep in New York City, MCAT Test Prep in Denver, ISEE Test Prep in Seattle, GRE Test Prep in Atlanta

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Calculus 3 : Vectors and Vector Operations

Study concepts, example questions & explanations for Calculus 3

All Calculus 3 Resources

Example Questions

Example Question #1 : Parametric Curves

Example Question #2 : Parametric Curves

Example Question #1 : Parametric Curves

Example Question #4 : Parametric Curves

Example Question #5 : Parametric Curves

Example Question #4 : Parametric Curves

Example Question #1 : Cross Product

Example Question #1 : Cross Product

Example Question #3 : Cross Product

Example Question #4 : Cross Product

All Calculus 3 Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: