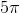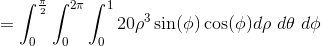All Calculus 3 Resources
Example Questions
Example Question #179 : Double Integrals
Example Question #180 : Double Integrals
Example Question #1551 : Calculus 3
Example Question #1552 : Calculus 3
Example Question #1552 : Calculus 3
Evaluate 

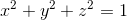
Since we are only dealing with the upper half of a sphere, we can determine the boundaries easily, and remember to convert to spherical coordinates.
Example Question #181 : Double Integrals
Calculate the following Integral.
Lets deal with the inner integral first.
Now we evaluate this expression in the outer integral.
Example Question #182 : Double Integrals
Calculate the definite integral of the function 
Cannot be solved.
Because there are no nested terms containing both 

This enables us to evaluate the double integral and the product of two independent single integrals. From the integration rules from single-variable calculus, we should arrive at the result

Example Question #3 : Double Integration Over General Regions
Evaluate the following integral on the region specified:
Where R is the region defined by the conditions:
Example Question #183 : Double Integrals
Evaluate:
Because the x and y terms in the integrand are independent of one another, we can move them to their respective integrals:
We used the following rules for integration:

Example Question #2 : Double Integration Over General Regions
Evaluate the following integral.
First, you must evaluate the integral with respect to y (because of the notation 
Using the rules of integration, this gets us

Evaluated from y=2 to y=3, we get

Integrating this with respect to x gets us 

All Calculus 3 Resources







![\begin{align*}&\theta_1=arctan(\frac{0.661}{-0.750})=0.77\pi;\theta_2=arctan(\frac{-0.861}{-0.509})=1.33\pi\\&\text{Now, utilizing integral rules:}\\&\int[rcos(ar^2)]=\frac{sin(ar^2)}{2a}\\&\int[rb^{ar^2}]=\frac{b^{ar^2}}{2aln(b)}\\&\int_{0.77\pi}^{1.33\pi}\int_{0.28}^{1.58}(\frac{(48\cdot r)}{(5\cdot (\frac{2}{7})^{(\frac{(2\cdot r^{2})}{3})})}- 32\cdot rcos(\frac{r^{2}}{2}))drd\theta=(- 32sin(\frac{r^{2}}{2}) -\frac{ 36}{(5\cdot (\frac{2}{7})^{(\frac{(2\cdot r^{2})}{3})}ln(\frac{2}{7}))})d\theta|_{0.28}^{1.58}\\&\int_{0.77\pi}^{1.33\pi}(11.0)d\theta=(11.0\theta)|_{0.77\pi}^{1.33\pi}=19.35\end{align*}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/775601/gif.latex)






![\begin{align*}&\theta_1=arctan(\frac{0.063}{0.998})=0.02\pi;\theta_2=arctan(\frac{0.996}{-0.094})=0.53\pi\\&\text{Now, utilizing integral rules:}\\&\int[rb^{ar^2}]=\frac{b^{ar^2}}{2aln(b)}\\&\int[re^{ar^2}]=\frac{e^{ar^2}}{2a}\\&\int_{0.02\pi}^{0.53\pi}\int_{0.34}^{1.91}(\frac{(2\cdot (\frac{7}{2})^{(\frac{(2\cdot r^{2})}{3})}\cdot r)}{25}+ re^{(\frac{(3\cdot r^{2})}{2})})drd\theta=(\frac{e^{(\frac{(3\cdot r^{2})}{2})}}{3}+\frac{ (3\cdot (\frac{7}{2})^{(\frac{(2\cdot r^{2})}{3})})}{(50ln(\frac{7}{2}))})d\theta|_{0.34}^{1.91}\\&\int_{0.02\pi}^{0.53\pi}(79.88)d\theta=(79.88\theta)|_{0.02\pi}^{0.53\pi}=127.99\end{align*}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/775577/gif.latex)






![\begin{align*}&\theta_1=arctan(\frac{0.790}{-0.613})=0.71\pi;\theta_2=arctan(\frac{-0.891}{-0.454})=1.35\pi\\&\text{Now, utilizing integral rules:}\\&\int[\frac{a}{r}]=aln(r)=ln(r^a)\\&\int_{0.71\pi}^{1.35\pi}\int_{0.22}^{1.31}(-\frac{50}{(3\cdot r)})drd\theta=(-\frac{(50ln(r))}{3})d\theta|_{0.22}^{1.31}\\&\int_{0.71\pi}^{1.35\pi}(-29.74)d\theta=(-29.74\theta)|_{0.71\pi}^{1.35\pi}=-59.79\end{align*}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/775631/gif.latex)






![\begin{align*}&\theta_1=arctan(\frac{0.613}{-0.790})=0.79\pi;\theta_2=arctan(\frac{-0.031}{1.000})=1.99\pi\\&\text{Now, utilizing integral rules:}\\&\int[rb^{ar^2}]=\frac{b^{ar^2}}{2aln(b)}\\&\int[rsin(ar^2)]=-\frac{cos(ar^2)}{2a}=-\frac{cos^2(\frac{a}{2}r^2)}{a}\\&\int_{0.79\pi}^{1.99\pi}\int_{0.41}^{1.71}(\frac{(19\cdot rsin(\frac{r^{2}}{2}))}{2}-\frac{ (47\cdot r)}{(4\cdot (\frac{2}{5})^{(r^{2})})})drd\theta=(\frac{47}{(8\cdot (\frac{2}{5})^{(r^{2})}ln(\frac{2}{5}))}-\frac{ (19cos(\frac{r^{2}}{2}))}{2})d\theta|_{0.41}^{1.71}\\&\int_{0.79\pi}^{1.99\pi}(-77.54)d\theta=(-77.54\theta)|_{0.79\pi}^{1.99\pi}=-292.31\end{align*}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/775607/gif.latex)