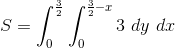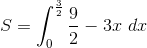All Calculus 3 Resources
Example Questions
Example Question #681 : Multiple Integration
Integrate:
To perform the iterated integration, we must work from inside outwards. To start we perform the following integration:
This becomes the integrand for the outermost integral:
Example Question #682 : Multiple Integration
To perform the iterated integral, we work from inside outwards.
The first integral we perform is
This becomes the integrand for the outermost integral,
Example Question #18 : Double Integration Over General Regions
Solve:
To evaluate the iterated integral, we must work from inside outward.
The first integral we evaluate is
This becomes the integrand for the outermost integral.
The final integral we evaluate is
Example Question #19 : Double Integration Over General Regions
.
Let 
![I=[a,b]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/914141/gif.latex)




3 and 4
1
1 3 and 4
1 and 3
1 and 4
1 and 3
No explanation necessary. This is the familiar integral for computing the area under the curve 
![[a,b]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/931506/gif.latex)
_____________________________________________________________
This integral does not give the area, in fact, it will result in a function of 
![I=[a,b]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/931507/gif.latex)
Now carry out the integration with respect to 
Certainly this is not the area of the area under 

_____________________________________________________________
This equation will reduce down to the first option, option 

Therefore, option 
___________________________________________________________
The problem with this choice can be seen immediately. Clearly the first integration in will simply be the area under the curve on 

![A = A[f(b)-f(a)]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/921381/gif.latex)



Example Question #20 : Double Integration Over General Regions
Evaluate the following iterated integrals:
When evaluating double integrals, work from the inside out: that is, evaluate the integrand with respect to the first variable listed by the differential operators, and then evaluate the result with respect to the second variable listed by the differential operators.
Here, we have the order of integration specified by 


Example Question #21 : Double Integration Over General Regions
Calculate the following Integral.
Lets deal with the inner integral first.
Now we evaluate this expression in the outer integral.
Example Question #22 : Double Integration Over General Regions
Calculate the following Integral.
Lets deal with the inner integral first.
Now we evaluate this expression in the outer integral.
Example Question #3821 : Calculus 3
Evaluate 



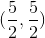

using the transformation 
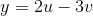
The first thing we have to do is figure out the general equations for the lines that create the trapezoid.
Now we have the general equations for out trapezoid, now we need to plug in our transformations into these equations.
So our region is a rectangle given by 
Next we need to calculate the Jacobian.
Now we can put the integral together.
Example Question #1 : Surface Area
Find the surface area of the part of the plane 
Lets recall the equation of surface area.
Now we need to find all the neccessary equations to be able to evaluate the integral.
We will plug in 
Now we are going to set 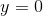
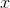
We now have all the bounds for our double integral
Certified Tutor
All Calculus 3 Resources




























![A = \int _0^{f(x)}\int_a^bdydx=\int_0^{f(x)}[y]_{y=a}^{y=b}dx=\int_0^{f(x)}(b-a)dx](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/921371/gif.latex)
![\int_0^{f(x)}(b-a)dx=\left[ (a-b)x\right ]_{x=0}^{x=f(x)}=(a-b)f(x)](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/921373/gif.latex)
![A = \int_a^b\int_0^{f(x)}dydx=\int_a^b \left[ \: \: y \, \, \right]_{y=o}^{y=f(x)} dx =\int_a^bf(x)dx](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/921366/gif.latex)
![A=\int_{f(a)}^{f(b)}\int_{a}^{b}f(x)dxdy = \int_{f(a)}^{f(b)}Ady = [Ay]_{y=f(a)}^{y=f(b)}=A[f(b)-f(a)]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/921380/gif.latex)







![=\int_-_1^3 \left [\int_0^\frac{\pi}{2} y^2 \cos(x) \ dx \right ] dy](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/877860/gif.latex)
![=\int_-_1^3 \left [y^2 \sin(x) \Big|_0^\frac{\pi}{2} \right ] dy](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1051524/gif.latex)
![=\int_-_1^3 \left [y^2 (1)-y^2(0) \right ] dy](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1051525/gif.latex)























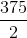


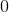



















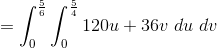

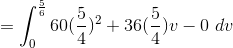







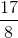
![S=\int \int_D \sqrt{[f_x]^2+[f_y]^2+1}\ dA](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/600202/gif.latex)


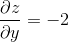


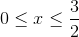

![S=\int_{0}^{\frac{3}{2}} \int_{0}^{\frac{3}{2}-x} \sqrt{[-2]^2+[-2]^2+1} \ dy \ dx](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/600215/gif.latex)