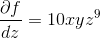All Calculus 3 Resources
Example Questions
Example Question #155 : Matrices
Find the determinant of the 3x3 matrix given:
To find the determinant of a 3x3 matrix 
Using the vectors from the problem statement, we get
Example Question #156 : Matrices
Find the determinant of the 3x3 matrix
To find the determinant of a 3x3 matrix 
Using the matrix from the problem statement, we get
Example Question #157 : Matrices
Find the determinant of the 3x3 matrix
To find the determinant of a 3x3 matrix 
Using the matrix from the problem statement, we get
Example Question #752 : Vectors And Vector Operations
Find the determinant of the matrix
To find the determinant of a 3x3 matrix 
Using the matrix from the problem statement, we get
Example Question #158 : Matrices
Calculate the determinant of Matrix 
In order to find the determinant of 
The next step is to multiply the down diagonals.
The next step is to multiply the up diagonals.
The last step is to substract 

Example Question #159 : Matrices
Calculate the determinant of Matrix 
In order to find the determinant of 
The next step is to multiply the down diagonals.
The next step is to multiply the up diagonals.
The last step is to substract 

Example Question #381 : Partial Derivatives
Find 
In order to find 




Natural Log:
Exponential Functions:
Power Functions:
Example Question #382 : Partial Derivatives
Find 
In order to find 




Natural Log:
Exponential Functions:
Power Functions:
Example Question #2751 : Calculus 3
Find 
In order to find 




Natural Log:
Exponential Functions:
Power Functions:
Example Question #392 : Partial Derivatives
True or False
False
True
True
True:
Since there are no 

Certified Tutor
All Calculus 3 Resources