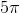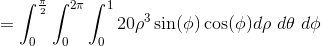All Calculus 3 Resources
Example Questions
Example Question #179 : Double Integrals
Example Question #180 : Double Integrals
Example Question #1551 : Calculus 3
Example Question #1552 : Calculus 3
Example Question #1 : Fundamental Theorem Of Line Integrals
Evaluate 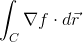


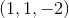

Since there isn't a specific path we need to take, we just evaluate 
Example Question #1551 : Calculus 3
Use Green's Theorem to evaluate 




First we need to make sure that the conditions for Green's Theorem are met.
The conditions are met because it is positively oriented, piecewise smooth, simple, and closed under the region (see below).
In this particular case 




We know from Green's Theorem that
So lets find the partial derivatives.
Example Question #1 : Green's Theorem
Use Green's Theorem to evaluate the line integral
over the region R, described by connecting the points 
Using Green's theorem
since the region is oriented clockwise, we would have
which gives us
Example Question #6 : Line Integrals
Use Greens Theorem to evaluate the line integral
over the region connecting the points 
Using Green's theorem

Since the region is oriented clockwise
Example Question #1552 : Calculus 3
Evaluate 

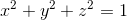
Since we are only dealing with the upper half of a sphere, we can determine the boundaries easily, and remember to convert to spherical coordinates.
Example Question #1 : Gradient Vector, Tangent Planes, And Normal Lines
Find the equation of the tangent plane to 

First, we need to find the partial derivatives in respect to 





Remember that the general equation for a tangent plane is as follows:
Now lets apply this to our problem
All Calculus 3 Resources







![\begin{align*}&\theta_1=arctan(\frac{0.661}{-0.750})=0.77\pi;\theta_2=arctan(\frac{-0.861}{-0.509})=1.33\pi\\&\text{Now, utilizing integral rules:}\\&\int[rcos(ar^2)]=\frac{sin(ar^2)}{2a}\\&\int[rb^{ar^2}]=\frac{b^{ar^2}}{2aln(b)}\\&\int_{0.77\pi}^{1.33\pi}\int_{0.28}^{1.58}(\frac{(48\cdot r)}{(5\cdot (\frac{2}{7})^{(\frac{(2\cdot r^{2})}{3})})}- 32\cdot rcos(\frac{r^{2}}{2}))drd\theta=(- 32sin(\frac{r^{2}}{2}) -\frac{ 36}{(5\cdot (\frac{2}{7})^{(\frac{(2\cdot r^{2})}{3})}ln(\frac{2}{7}))})d\theta|_{0.28}^{1.58}\\&\int_{0.77\pi}^{1.33\pi}(11.0)d\theta=(11.0\theta)|_{0.77\pi}^{1.33\pi}=19.35\end{align*}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/775601/gif.latex)






![\begin{align*}&\theta_1=arctan(\frac{0.063}{0.998})=0.02\pi;\theta_2=arctan(\frac{0.996}{-0.094})=0.53\pi\\&\text{Now, utilizing integral rules:}\\&\int[rb^{ar^2}]=\frac{b^{ar^2}}{2aln(b)}\\&\int[re^{ar^2}]=\frac{e^{ar^2}}{2a}\\&\int_{0.02\pi}^{0.53\pi}\int_{0.34}^{1.91}(\frac{(2\cdot (\frac{7}{2})^{(\frac{(2\cdot r^{2})}{3})}\cdot r)}{25}+ re^{(\frac{(3\cdot r^{2})}{2})})drd\theta=(\frac{e^{(\frac{(3\cdot r^{2})}{2})}}{3}+\frac{ (3\cdot (\frac{7}{2})^{(\frac{(2\cdot r^{2})}{3})})}{(50ln(\frac{7}{2}))})d\theta|_{0.34}^{1.91}\\&\int_{0.02\pi}^{0.53\pi}(79.88)d\theta=(79.88\theta)|_{0.02\pi}^{0.53\pi}=127.99\end{align*}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/775577/gif.latex)






![\begin{align*}&\theta_1=arctan(\frac{0.790}{-0.613})=0.71\pi;\theta_2=arctan(\frac{-0.891}{-0.454})=1.35\pi\\&\text{Now, utilizing integral rules:}\\&\int[\frac{a}{r}]=aln(r)=ln(r^a)\\&\int_{0.71\pi}^{1.35\pi}\int_{0.22}^{1.31}(-\frac{50}{(3\cdot r)})drd\theta=(-\frac{(50ln(r))}{3})d\theta|_{0.22}^{1.31}\\&\int_{0.71\pi}^{1.35\pi}(-29.74)d\theta=(-29.74\theta)|_{0.71\pi}^{1.35\pi}=-59.79\end{align*}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/775631/gif.latex)






![\begin{align*}&\theta_1=arctan(\frac{0.613}{-0.790})=0.79\pi;\theta_2=arctan(\frac{-0.031}{1.000})=1.99\pi\\&\text{Now, utilizing integral rules:}\\&\int[rb^{ar^2}]=\frac{b^{ar^2}}{2aln(b)}\\&\int[rsin(ar^2)]=-\frac{cos(ar^2)}{2a}=-\frac{cos^2(\frac{a}{2}r^2)}{a}\\&\int_{0.79\pi}^{1.99\pi}\int_{0.41}^{1.71}(\frac{(19\cdot rsin(\frac{r^{2}}{2}))}{2}-\frac{ (47\cdot r)}{(4\cdot (\frac{2}{5})^{(r^{2})})})drd\theta=(\frac{47}{(8\cdot (\frac{2}{5})^{(r^{2})}ln(\frac{2}{5}))}-\frac{ (19cos(\frac{r^{2}}{2}))}{2})d\theta|_{0.41}^{1.71}\\&\int_{0.79\pi}^{1.99\pi}(-77.54)d\theta=(-77.54\theta)|_{0.79\pi}^{1.99\pi}=-292.31\end{align*}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/775607/gif.latex)





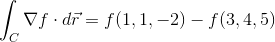

























![\int_C{F}dr=\int \int\left[{\frac{\partial{Q}}{\partial{x}}-\frac{\partial{P}}{\partial{y}}}\right]dA](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/766279/gif.latex)


![\int_C{F}dr=-\int\int\left[\frac{\partial{Q}}{\partial{x}}-\frac{\partial{P}}{\partial{y}}\right]dA](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/766282/gif.latex)







![\int_C F dr=\int\int \left[\frac{\partial{Q}}{\partial{x}}-\frac{\partial{P}}{\partial{y}}\right]dA](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/768557/gif.latex)