Step 1: Recall any rules that are used in derivatives...

• Power Rule
• Quotient Rule
• Product Rule
• Chain Rule

Step 2: Look at the choices in the question and compare the ones listed in Step 1.

We see Power Rule, Chain Rule, and Product Rule.

There is no such rule called the Addition rule, so this is the incorrect answer.

This is a conceptual problem. First notice that the function  is the sum of two functions  and . We must differentiate each term. 

To differentiate the first term, notice that  is a function of the function , so we must use the chain rule to differentiate with respect to . We cannot conclude that . 

We were given . What this equation is telling us is that the function   will have a derivative that is 2 times whatever is inside the parenthesis, with respect to the whatever is inside the parenthesis. If we wish to use  to differentiate the composite   we can start with the derivative with respect to  , which will be .

Now if we want to differentiate with respect to , we take the derivative with respect to  and multiply by the derivative of  with respect to   (the chain rule). 

We were given

Now we can write the derivative of , 

Find the equation of the tangent line to the curve corresponding to 

The first step is to compute the derivative for the function and then evaluate the derivative at 

Therefore  will be the slope of the tangent line at . Write an equation for the line,  

Now we need to find the y-intercept. Use the original function to find  when . 

This gives us the point at which the tangent line meets the curve, 

Now use this point to find the y-intercept, 

. 

The equation of the line is therefore, 

First we see from the sum rule that:

The first term we use the product rule to differentiate:

The second term is:

Therefore:

To differentiate the function y=ln(cos(x)) we have to use the chain rule

 let u=cos(x)  therefore y=ln(u) and

and

Therefore:

First we simplify the function using properties of logarithmic functions:

   and 

Therefore:

also

Therefore    

and

to derive this equation we use the product rule:

and

Therefore:

Logarithmic differentiation exploits the properties of logarithms to easily compute derivatives for functions that would otherwise be extremely tedious to find. Direct differentiation using the quotient rule could become quite messy. Take the natural logarithm of both sides of the equation, 

                               (1)

Expand the right-side using the properties of logarithms:

____________________________________________________________

Properties of Logarithmic Functions:

1. 

2. 

3. 

Then proceed with the differentiation using the known derivative of the natural logarithm function and the chain rule: 

____________________________________________________________

Derivative of the Natural Logarithm 

For a function  of , apply the chain-rule, 

____________________________________________________________

Expanding the right-side of equation (1) first by using Property 2. 

Expand the second term with Property 1. Use Property 3 to pull out the exponent in the third term obtained after applying Property 1. 

Differentiating implicitly over both sides of the equation with respect to . Be sure to apply the chain rule as needed. 

So now the derivative we were looking for,  can be solved by multiplying both sides by  and then substituting back in the original function to write everything in terms of 

The farmer's fencing material needs to cover the perimeter of his property. Since this piece of property is shaped like a rectangle, we know that the perimeter can be modeled with the equation

.

In this case, we know that , since the  ft. of fencing need to fit around the whole property.

This problem wants to maximize the area, so we're trying to find which values maximize this equation:

.

We know that 

, or simplified, that .

Solving for  gives us 

,

which we can plug into our area equation, giving us

.

Taking the first derivative gives us 

.

Making  equal zero allows us to solve for . 

.

So,  is 175 ft. To determine if this value is a maximum length, or a minimum, we take the second derivative of our area equation, which yields a constant. Because this value is always less than zero, 175 ft. is a maximum. using our perimeter formula, we see that  is also equal to 175 ft. So, the maximum area the farmer can fence off is 175 ft. x 175 ft., or 30,625  sq. ft.

on this problem we apply the product rule:

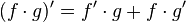
let:       and