Call Now to Set Up Tutoring:

(888) 888-0446

Calculus 2 : Calculus II

Study concepts, example questions & explanations for Calculus 2

Create An Account

All Calculus 2 Resources

9 Diagnostic Tests 308 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #461 : Derivative Review

Define $f (x,y) = e ^{x^{2}+ y^{2}}$ .

Find $f _{xy} (x,y)$ .

Possible Answers:

$f _{xy} (x,y)= 4xy e ^{x^{2}+y^{2}}$

$f _{xy} (x,y)= xy e ^{x^{2}+y^{2}}$

$f _{xy} (x,y)=2 xy e ^{x^{2}+y^{2}}$

$f _{xy} (x,y)= xe ^{x^{2}+y^{2}} + y e ^{x^{2}+y^{2}}$

$f _{xy} (x,y)=2xe ^{x^{2}+y^{2}} + 2y e ^{x^{2}+y^{2}}$

Correct answer:

$f _{xy} (x,y)= 4xy e ^{x^{2}+y^{2}}$

Explanation:

First, find $f_{x} = \frac{\partial f}{\partial x}$ as follows:

$f (x,y) = e ^{x^{2}+ y^{2}} = e ^{x^{2} } e ^{y^{2} }$

$\frac{\partial }{\partial x}f (x,y) = \frac{\partial }{\partial x} \left (e ^{x^{2} } e ^{y^{2} } \right )$

$= e ^{y^{2}} \cdot \frac{\partial }{\partial x} \left (e ^{x^{2} }} \right )$

$= e ^{y^{2}} \cdot \frac{\partial }{\partial x} x^{2} \cdot \left (e ^{x^{2} }} \right )$

$= 2x \cdot e ^{y^{2}} \cdot \left (e ^{x^{2} }} \right )$

$= 2x e ^{x^{2}} e ^{y^{2}}$

Therefore, $f_{x} (x,y ) = 2x e ^{x^{2}} e ^{y^{2}}$ .

Now, find $f_{xy} = \frac{\partial }{\partial y} f_{x}$ as follows:

$f_{x} (x,y )= 2x e ^{x^{2}} e ^{y^{2}}$

$\frac{\partial }{\partial y} f_{x} (x,y ) = \frac{\partial }{\partial y} \left ( 2x e ^{x^{2}} e ^{y^{2}} \right )$

$=2x e ^{x^{2}} \frac{\partial }{\partial y} \left ( e ^{y^{2}} \right )$

$=2x e ^{x^{2}} \frac{\partial }{\partial y} \left ( y^{2} \right ) e ^{y^{2}}$

$=2x e ^{x^{2}} \cdot 2y \cdot e ^{y^{2}}$

$=4xy e ^{x^{2}} e ^{y^{2}} = 4xy e ^{x^{2}+y^{2}}$

Report an Error

Example Question #461 : Derivatives

Define $f (x,y) = \cos (x^{2} + y^{2})$ .

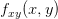
Find $f _{xy} (x,y)$ .

Possible Answers:

$f _{xy} (x,y) = 4x \cos (x^{2} + y^{2}) + 4y \cos (x^{2} + y^{2})$

$f _{xy} (x,y) =- 4x \cos (x^{2} + y^{2}) + 4y \cos (x^{2} + y^{2})$

$f _{xy} (x,y) =- 4xy \cos (x^{2} + y^{2})$

$f _{xy} (x,y) = 4xy \cos (x^{2} + y^{2})$

$f _{xy} (x,y) = 4x \cos (x^{2} + y^{2}) - 4y \cos (x^{2} + y^{2})$

Correct answer:

$f _{xy} (x,y) =- 4xy \cos (x^{2} + y^{2})$

Explanation:

First, find $f_{x} = \frac{\partial f}{\partial x}$ as follows:

$f (x,y) = \cos (x^{2} + y^{2})$

$\frac{\partial }{\partial x}f (x,y) = \frac{\partial }{\partial x} \cos (x^{2} + y^{2})$

$= \frac{\partial }{\partial x}(x^{2} + y^{2}) \cdot \left [ - \sin (x^{2} + y^{2}) \right ]$

$= (2x + 0) \cdot \left [ - \sin (x^{2} + y^{2}) \right ]$

$= - 2x\sin (x^{2} + y^{2})$

Therefore, $f_{x} (x,y ) = - 2x\sin (x^{2} + y^{2})$ .

Now, find $f_{xy} = \frac{\partial }{\partial y} f_{x}$ as follows:

$f_{x} (x,y ) = - 2x\sin (x^{2} + y^{2})$

$\frac{\partial }{\partial y} f_{x} (x,y ) = \frac{\partial }{\partial y}\left [ - 2x\sin (x^{2} + y^{2}) \right ]$

$=- 2x \frac{\partial }{\partial y}\left [ \sin (x^{2} + y^{2}) \right ]$

$=- 2x\cdot \frac{\partial }{\partial y}(x^{2} + y^{2}) \cdot \cos (x^{2} + y^{2})$

$=- 2x\cdot (0 + 2y) \cdot \cos (x^{2} + y^{2})$

$=- 2x\cdot ( 2y) \cdot \cos (x^{2} + y^{2})$

$=- 4xy \cos (x^{2} + y^{2})$

Report an Error

Example Question #1591 : Calculus Ii

Define $f (x,y) = \log xy$ .

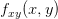
Find $f _{xy} (x,y)$ .

Possible Answers:

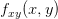
$f _{xy} (x,y) = \frac{x+y}{x y}$

$f _{xy} (x,y) = 1$

$f _{xy} (x,y) = \frac{1}{x+y}$

$f _{xy} (x,y) = 0$

$f _{xy} (x,y) = \frac{1}{xy}$

Correct answer:

$f _{xy} (x,y) = 0$

Explanation:

First, find $f_{x} = \frac{\partial f}{\partial x}$ as follows:

$f (x,y) = \log xy = \log x + \log y = \frac{ \ln x }{\ln 10}+ \frac{ \ln y }{\ln 10}$

$f (x,y) = \frac{ 1}{\ln 10}\left ( \ln x+ \ln y \right )$

$\frac{\partial }{\partial x}f (x,y) = \frac{\partial }{\partial x}\left [ \frac{ 1}{\ln 10}\left ( \ln x+ \ln y \right ) \right ]$

$= \frac{ 1}{\ln 10} \left (\frac{\partial }{\partial x}\left \ln x+\frac{\partial }{\partial x} \ln y \right )$

$= \frac{ 1}{\ln 10} \left ( \frac{1}{x}+0 \right )$

$= \frac{ 1}{\ln 10} \cdot \frac{1}{x}$

Therefore, $f_{x} (x,y )= \frac{ 1}{\ln 10} \cdot \frac{1}{x}$ .

Now, find $f_{xy} = \frac{\partial }{\partial y} f_{x}$ as follows:

$f_{x} (x,y )= \frac{ 1}{\ln 10} \cdot \frac{1}{x}$

$\frac{\partial }{\partial y} f_{x} (x,y ) = \frac{\partial }{\partial y}\left ( \frac{ 1}{\ln 10} \cdot \frac{1}{x} \right )$

Report an Error

Example Question #462 : Derivatives

Let the initial approximation of a solution of the equation

$e^{x} = \sin x$

be $x_{1} = -2$ .

Use one iteration of Newton's method to find an approximation for $x_{2}$ . Give your answer to the nearest thousandth.

Possible Answers:

-4.095

-3.795

-4.195

-3.695

-3.895

Correct answer:

-3.895

Explanation:

Rewrite the equation to be solved for as $e^{x} - \sin x = 0$ .

Let $f(x ) = e^{x} - \sin x$ .

$f'(x ) = \frac{\mathrm{d} }{\mathrm{d} x} \left (e^{x} - \sin x \right )$

$f'(x ) = e^{x} - \cos x \right )$

The problem amounts to finding a zero of f(x ) . By Newton's method, the second approximation can be derived from the first using the equation

$x_{2} = x_{1} - \frac{f(x_{1})}{f'(x_{1})}$ .

Since $x_{1} = -2$ ,

$f(-2 ) = e^{-2} - \sin (-2) \approx 0.1353 - (-0.9093 ) \approx 1.0446$

and

$f'(-2 ) = e^{-2} - \cos (-2) \approx 0.1353 - \left ( -0.4161 \right )\approx 0.5514$

Use these to find the approximation:

$x_{2} =-2 - \frac{f(-2)}{f'(-2)} \approx -2 - \frac{1.0446}{0.5514}\approx -2 -1.8945 \approx -3.895$

Report an Error

Example Question #467 : Derivative Review

Define f(x) = e^x- 4x .

Give the minimum value of on the set of all real numbers.

Possible Answers:

$4 - 4 \ln 4$

$2- 4 \ln 2$

The function has no miminum value.

e^4 - 16

e^2 - 4

Correct answer:

$4 - 4 \ln 4$

Explanation:

This function is continuous and differentiable everywhere. First we find the value(s) of for which f'(x) =0 .

f(x) = e^x- 4x

$f'(x) =\frac{\mathrm{d} }{\mathrm{d} x}\left ( e^x- 4x \right )$

f'(x) = e^x- 4

f'(x) =0

e^x- 4 =0

e^x= 4

$\ln e^x= \ln 4$

$x= \ln 4$

Therefore, this is the only possible minimum. We determine whether it is a minimum by evaluating $f''(\ln 4)$ :

f'(x) = e^x- 4

$f''(x) = \frac{\mathrm{d} }{\mathrm{d} x} \left ( e^x- 4 \right )$

f''(x) = e^x

$f''(\ln 4) = e^{\ln 4} = 4 > 0$

Since $f''(\ln 4) > 0$ , has its minimum value at $x= \ln 4$ ; it is

$f( \ln 4) = e^{ \ln 4}- 4 \cdot \ln 4 = 4 - 4 \ln 4$ .

Report an Error

Example Question #1592 : Calculus Ii

Consider the equation

$y =\ln \left ( \sin x + \cos y \right )$ .

Which of the following is equal to $\frac{\mathrm{d} y}{\mathrm{d} x}$ ?

Possible Answers:

$\frac{\mathrm{d} y }{\mathrm{d} x} =\frac{ \sin x}{ \sin x + \cos x + \cos y }$

$\frac{\mathrm{d} y }{\mathrm{d} x} =\frac{ \cos x}{ \sin x + \sin y + \cos y }$

$\frac{\mathrm{d} y }{\mathrm{d} x} =\frac{ \cos x}{ \sin x + \cos x + \cos y }$

$\frac{\mathrm{d} y }{\mathrm{d} x} =\frac{ \sin x}{ \sin x + \sin y + \cos y }$

$\frac{\mathrm{d} y }{\mathrm{d} x} =\frac{ \sin x + \cos x}{ \sin y + \cos y }$

Correct answer:

$\frac{\mathrm{d} y }{\mathrm{d} x} =\frac{ \cos x}{ \sin x + \sin y + \cos y }$

Explanation:

$y =\ln \left ( \sin x + \cos y \right )$

$\frac{\mathrm{d} y }{\mathrm{d} x}= \frac{\mathrm{d} }{\mathrm{d} x}\ln \left ( \sin x + \cos y \right )$

$\frac{\mathrm{d} y }{\mathrm{d} x}= \frac{\frac{\mathrm{d} }{\mathrm{d} x} \left ( \sin x + \cos y \right )}{\sin x + \cos y}$

$\frac{\mathrm{d} y }{\mathrm{d} x} \left ( \sin x + \cos y \right )= \frac{\mathrm{d} }{\mathrm{d} x} \left ( \sin x + \cos y \right )$

$\frac{\mathrm{d} y }{\mathrm{d} x} \sin x + \frac{\mathrm{d} y }{\mathrm{d} x} \cos y \right )= \cos x - \frac{\mathrm{d}y }{\mathrm{d} x} \sin y$

$\frac{\mathrm{d} y }{\mathrm{d} x} \sin x + \frac{\mathrm{d}y }{\mathrm{d} x} \sin y+ \frac{\mathrm{d} y }{\mathrm{d} x} \cos y \right )= \cos x$

$\frac{\mathrm{d} y }{\mathrm{d} x} \left (\sin x + \sin y+ \cos y \right )= \cos x$

$\frac{\mathrm{d} y }{\mathrm{d} x} =\frac{ \cos x}{ \sin x + \sin y+ \cos y }$

Report an Error

Example Question #1593 : Calculus Ii

Define $f(x) = 4x + 8 \sin x$ .

Give the minimum value of f(x) on the interval $[-\pi, \pi]$ .

Possible Answers:

$-\frac{4}{3} \pi - 4$

$-\frac{8}{3} \pi - 4 \sqrt {3}$

$-4 \pi$

Correct answer:

$-\frac{8}{3} \pi - 4 \sqrt {3}$

Explanation:

$f(x) = 4x + 8 \sin x$

$f'(x) = 4 + 8 \cos x$

We first look for such that f'(x) = 0 :

$4 + 8 \cos x = 0$

$8 \cos x = -4$

$\cos x = -\frac{1}{2}$

The two values on the interval $[-\pi, \pi]$ for which this holds true are $-\frac{2}{3} \pi , \frac{2}{3} \pi$ , so we evaluate for the values $- \pi, -\frac{2}{3} \pi , \frac{2}{3} \pi, \pi$ :

$f(-\pi ) = 4(-\pi ) + 8 \sin (-\pi ) = -4 \pi + 8 \cdot 0 = -4 \pi \approx -12. 5$

$f \left $-\frac{2}{3} \pi\right $ = 4\left $-\frac{2}{3} \pi\right $ + 8 \sin \left $-\frac{2}{3} \pi\right $$

$= -\frac{8}{3} \pi + 8 \cdot \left (- \frac{\sqrt{3}}{2} \right ) = -\frac{8}{3} \pi - 4 \sqrt {3} \approx -15.3$

$f \left $\frac{2}{3} \pi\right $ = 4\left $\frac{2}{3} \pi\right $ + 8 \sin \left $\frac{2}{3} \pi\right $$

$= \frac{8}{3} \pi + 8 \cdot \left ( \frac{\sqrt{3}}{2} \right ) = \frac{8}{3} \pi + 4 \sqrt {3} \approx 15.3$

$f(\pi ) = 4\pi + 8 \sin \pi = 4 \pi + 8 \cdot 0 = 4 \pi \approx 12. 5$

The minimum value is $f \left $-\frac{2}{3} \pi\right $ = -\frac{8}{3} \pi - 4 \sqrt {3}$ .

Report an Error

Example Question #1594 : Calculus Ii

Consider the equation

$x^2 + y^2 = e^ { xy }$ .

Which of the following is equal to $\frac{\mathrm{d} y}{\mathrm{d} x}$ ?

Possible Answers:

$\frac{\mathrm{d} y}{\mathrm{d} x} =\frac{ 2x+ y e^ { xy } }{2y- x e^ { xy }}$

$\frac{\mathrm{d} y}{\mathrm{d} x} =\frac{ 2x+ 2y }{x e^ { xy }- y e^ { xy }}$

$\frac{\mathrm{d} y}{\mathrm{d} x} =\frac{ 2x+ 2y }{y e^ { xy }- x e^ { xy }}$

$\frac{\mathrm{d} y}{\mathrm{d} x} =\frac{ 2x- y e^ { xy } }{2y- x e^ { xy }}$

$\frac{\mathrm{d} y}{\mathrm{d} x} =\frac{ -2x+ y e^ { xy } }{2y- x e^ { xy }}$

Correct answer:

$\frac{\mathrm{d} y}{\mathrm{d} x} =\frac{ -2x+ y e^ { xy } }{2y- x e^ { xy }}$

Explanation:

$x^2 + y^2 = e^ { xy }$

$\frac{\mathrm{d} }{\mathrm{d} x}\left ( x^2 + y^2 \right )= \frac{\mathrm{d} }{\mathrm{d} x}e^ { xy }$

$2x + 2y \frac{\mathrm{d} y}{\mathrm{d} x} = \frac{\mathrm{d} }{\mathrm{d} x} xy \cdot e^ { xy }$

$2x + 2y\cdot \frac{\mathrm{d} y}{\mathrm{d} x} = \left ( x \cdot \frac{\mathrm{d}y }{\mathrm{d} x} + y \right ) \cdot e^ { xy }$

$2x + 2y\cdot \frac{\mathrm{d} y}{\mathrm{d} x} = x e^ { xy }\cdot \frac{\mathrm{d}y }{\mathrm{d} x} + y e^ { xy }$

$2y\cdot \frac{\mathrm{d} y}{\mathrm{d} x} - x e^ { xy }\cdot \frac{\mathrm{d}y }{\mathrm{d} x} =-2x+ y e^ { xy }$

$\left (2y- x e^ { xy } \right )\cdot \frac{\mathrm{d} y}{\mathrm{d} x} =-2x+ y e^ { xy }$

$\frac{\mathrm{d} y}{\mathrm{d} x} =\frac{ -2x+ y e^ { xy } }{2y- x e^ { xy }}$

Report an Error

Example Question #1 : Finding Maximums

Define $f(x) = \frac{x}{2}+ \sin x$ .

Give the maximum value of f(x) on the interval $[0, \pi]$ .

Possible Answers:

$\frac{\pi}{2}$

$\frac{\pi + 2\sqrt{2}}{4}$

$\frac{3\pi + 2\sqrt{2}}{4}$

$\frac{ 2\pi + 3\sqrt{3} }{6}$

$\frac{ \pi + 3\sqrt{3} }{6}$

Correct answer:

$\frac{ 2\pi + 3\sqrt{3} }{6}$

Explanation:

First, we determine if there are any points at which f'(x) = 0 .

$f(x) = \frac{x}{2}+ \sin x = \frac{1}{2}x+ \sin x$

$f'(x) = \frac{1}{2} + \cos x$

f'(x) = 0

$\frac{1}{2} + \cos x = 0$

$\cos x = -\frac{1}{2}$

The only point on the interval on which this is true is $x =\frac{ 2\pi }{3}$ .

We test this point as well as the two endpoints, x = 0 and $x = \pi$ , by evaluating for each of these values.

$f(0) = \frac{0}{2}+ \sin 0 = 0 + 0 = 0$

$f\left ( \frac{ 2\pi }{3} \right ) = \frac{ \left ( \frac{ 2\pi }{3} \right )}{2}+ \sin \frac{ 2\pi }{3} = \frac{ \pi }{3} + \frac{\sqrt{3}}{2} \approx 2$

$f( \pi ) = \frac{ \pi}{2}+ \sin \pi = \frac{ \pi}{2} + 0 = \frac{ \pi}{2} \approx 1.6$

Therefore, assumes its maximum on this interval at the point $x =\frac{ 2\pi }{3}$ , and $f\left ( \frac{ 2\pi }{3} \right ) = \frac{ \pi }{3} + \frac{\sqrt{3}}{2} = \frac{ 2\pi + 3\sqrt{3} }{6}$ .

Report an Error

Example Question #1591 : Calculus Ii

Consider the equation

$\sec y = x^2 + xy^2$ .

Which of the following is equal to $\frac{\mathrm{d} y}{\mathrm{d} x}$ ?

Possible Answers:

$\frac{\mathrm{d}y }{\mathrm{d} x} =\frac{2x + y^2}{ \sec y \tan y - 2xy}$

$\frac{\mathrm{d}y }{\mathrm{d} x} =\frac{2x + y^2}{ \sec y \tan y + 2xy}$

$\frac{\mathrm{d}y }{\mathrm{d} x} =\frac{2x + y^2}{ \sec ^2 y - 2xy}$

$\frac{\mathrm{d}y }{\mathrm{d} x} =\frac{2x - y^2}{ \sec y \tan y - 2xy}$

$\frac{\mathrm{d}y }{\mathrm{d} x} =\frac{2x - y^2}{ \sec ^2 y - 2xy}$

Correct answer:

$\frac{\mathrm{d}y }{\mathrm{d} x} =\frac{2x + y^2}{ \sec y \tan y - 2xy}$

Explanation:

$\sec y = x^2 + xy^2$

$\frac{\mathrm{d} }{\mathrm{d} x} \sec y =\frac{\mathrm{d} }{\mathrm{d} x} \left (x^2 + xy^2 \right )$

$\frac{\mathrm{d}y }{\mathrm{d} x} \sec y \tan y=2x + y^2 + x \cdot 2y \cdot \frac{\mathrm{d}y }{\mathrm{d} x}$

$\frac{\mathrm{d}y }{\mathrm{d} x} \sec y \tan y=2x + y^2 + 2xy \frac{\mathrm{d}y }{\mathrm{d} x}$

$\frac{\mathrm{d}y }{\mathrm{d} x} \sec y \tan y - \frac{\mathrm{d}y }{\mathrm{d} x} 2xy=2x + y^2$

$\frac{\mathrm{d}y }{\mathrm{d} x} =\frac{2x + y^2}{ \sec y \tan y - 2xy}$

Report an Error

View Calculus 2 Tutors

Mayowa
Certified Tutor

Logan University, Bachelor of Science, Biology, General.

View Calculus 2 Tutors

Luis
Certified Tutor

State University of New York at New Paltz, Doctor of Science, Health Physics.

View Calculus 2 Tutors

Michael
Certified Tutor

University of Richmond, Bachelor of Science, Mathematics. Central Connecticut State University, Master of Arts, Mathematics.

All Calculus 2 Resources

9 Diagnostic Tests 308 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Chemistry Tutors in San Francisco-Bay Area, Math Tutors in Denver, Algebra Tutors in Washington DC, MCAT Tutors in Dallas Fort Worth, Computer Science Tutors in Atlanta, English Tutors in Philadelphia, Calculus Tutors in Seattle, Spanish Tutors in Seattle, Calculus Tutors in Denver, SAT Tutors in Seattle

Popular Courses & Classes

SAT Courses & Classes in Phoenix, ISEE Courses & Classes in Los Angeles, GMAT Courses & Classes in Miami, GMAT Courses & Classes in Washington DC, LSAT Courses & Classes in Seattle, Spanish Courses & Classes in Boston, GMAT Courses & Classes in Houston, ACT Courses & Classes in San Diego, LSAT Courses & Classes in Houston, GMAT Courses & Classes in Chicago

Popular Test Prep

ACT Test Prep in San Diego, LSAT Test Prep in Miami, SSAT Test Prep in Los Angeles, ISEE Test Prep in Miami, ACT Test Prep in Philadelphia, MCAT Test Prep in Philadelphia, MCAT Test Prep in Miami, ISEE Test Prep in Atlanta, ACT Test Prep in Chicago, GMAT Test Prep in Washington DC

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Calculus 2 : Calculus II

Study concepts, example questions & explanations for Calculus 2

All Calculus 2 Resources

Example Questions

Example Question #461 : Derivative Review

Example Question #461 : Derivatives

Example Question #1591 : Calculus Ii

Example Question #462 : Derivatives

Example Question #467 : Derivative Review

Example Question #1592 : Calculus Ii

Example Question #1593 : Calculus Ii

Example Question #1594 : Calculus Ii

Example Question #1 : Finding Maximums

Example Question #1591 : Calculus Ii

All Calculus 2 Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: