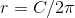Call Now to Set Up Tutoring:

(888) 888-0446

Basic Geometry : Plane Geometry

Study concepts, example questions & explanations for Basic Geometry

Create An Account

All Basic Geometry Resources

9 Diagnostic Tests 164 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #371 : Basic Geometry

Use 3.14 for Pi in the following question.

If the circumference of a circle is 25.12cm, what is the measure of its diameter?

Possible Answers:

$12.5\text{ cm}$

$11.3\text{ cm}$

$8\text{ cm}$

$6\text{ cm}$

$21.98\text{ cm}$

Correct answer:

$8\text{ cm}$

Explanation:

First we need to know that the formula for circumference of a circle is

$\text{Circumference}=\text{Diameter}\cdot \pi$ .

Since we know the circumference, we can plug it into our equation, along with pi, and solve for diameter.

$25.12cm=D\cdot3.14$

To solve for D (diameter) we must divide both sides by pi

$25.12cm\div3.14=D$

when we divide 25.12 by 3.14 we get 8, so our final answer is 8cm.

Report an Error

Example Question #372 : Basic Geometry

A circular pizza has an area of $36\pi$ square inches. What is its diameter in inches?

Possible Answers:

Correct answer:

Explanation:

The area of a circle with a given radius is $A=\pi r^2$ . Since the area of the circular pizza is given as $36\pi$ square inches, we can solve for its radius as follows:

$36\pi=\pi r^2$

$\Rightarrow 36 = r^2$

$\Rightarrow r = \sqrt{36} = 6$

Now that we know that the radius of the pizza is inches, we can now deduce its diameter knowing that the diameter of a circle is equal to twice its radius. Hence, the diameter of this pizza is 2(6)=12 inches.

Report an Error

Example Question #1 : How To Find The Ratio Of Diameter And Circumference

Let represent the area of a circle and represent its circumference. Which of the following equations expresses in terms of ?

Possible Answers:

C^2

Correct answer:

Explanation:

The formula for the area of a circle is $A=\pi r^2$ , and the formula for circumference is $C=2\pi r$ . If we solve for C in terms of r, we get
$r=C/2\pi$ .

We can then substitute this value of r into the formula for the area:

$A=\pi r^2$

$=\pi (C/2\pi )^2$

$=C^2\pi /4\pi ^2$

$=C^2/4\pi$

Report an Error

Example Question #1 : How To Find The Ratio Of Diameter And Circumference

A can of soup has a base area of $16\pi$ . What is the ratio of the can's diameter to its circumference?

Possible Answers:

$\frac{1}{2\pi}$

$\frac{\pi}{8}$

$\frac{\pi}{1}$

$\frac{2\pi}{1}$

$\frac{1}{\pi}$

Correct answer:

$\frac{1}{\pi}$

Explanation:

If the cirlcle has an area of $16\pi$ then we need to find a way to determine the diameter of the circle. We must do 4 things:

1. Find the radius of the circle since all we know is the area of the circle.

2. Double the radius to find the diameter.

3. Find the circumference by $C=\pi d$

4. Write the ratio

$A_{circle}=\pi r^2$

$16\pi=\pi r^2$

Solving to find the radius we get:

16=r^2

4=r

So if the radius is 4 then the diameter is:

d=2(4)=8

Then the circumference is:

$C=8\pi$

The ratio of the diameter to the circumference is:

$\frac{d}{C}=\frac{8}{8\pi}=\frac{1}{\pi}$

Report an Error

Example Question #371 : Basic Geometry

The circumference of the base of a silo is $144\pi$ ft. What is the ratio of the silo's circumference to its diameter?

Possible Answers:

1:144

$144:\pi$

$\pi:1$

$1:\pi$

144:1

Correct answer:

$\pi:1$

Explanation:

Since the silo has base circumference of $144\pi$ , then according to the formula for the circumference of a circle:

$C=\pi d$

$144\pi=\pi d$

Solving for diameter:

144=d

So the diameter is 144 ft. Therefore the ratio of the circumference to the diameter would be:

$144\pi:144\rightarrow \pi:1$

Report an Error

Example Question #2 : How To Find The Ratio Of Diameter And Circumference

The diameter of a certain circle is tripled. Compared to the circumference of the original circle, how many times as large is the circumference of the new circle?

Possible Answers:

$3\pi$

$9\pi$

Correct answer:

Explanation:

The easiest way to find our answer is to try actual values. Imagine we have a circle with a diameter of . Given the formula for circumference

$C=d\pi$

our circumference is simply $2\pi$ . Tripling the diameter gives a new diameter of and therefore a new circumference of $6\pi$ . We can then determine the ratio between the two circumferences.

$\frac{6\pi}{2\pi}=3$

Therefore, the new circumference is 3 times as large as the old.

Report an Error

Example Question #372 : Basic Geometry

Find the ratio of the diameter to the circumference in a circle with radius r.

Possible Answers:

$\pi$

$2\pi{r}$

$\frac{1}{\pi}$

Correct answer:

$\frac{1}{\pi}$

Explanation:

To find a ratio, simply divide your two quantities. Remember,

D=2r

$C=2\pi{r}$

Thus,

$ratio=\frac{D}{C}=\frac{2r}{2\pi{r}}=\frac{1}{\pi}$

Report an Error

Example Question #72 : Diameter

What is the circumference to diameter ratio of a circle with a diameter of 15?

Possible Answers:

3.14

4.75

3.75

Cannot be determined.

4.14

Correct answer:

3.14

Explanation:

First you must find the circumference of a circle with a diameter of 15 with the formula $C=\pi*D$ .

$C=\pi*15=47.1$

Since the ratio of C to D is represented by $\pi=\frac{C}{D}$ , all of the ratios of Circumference to Diameter should approximately equal $\pi$ .

$\frac{47.1}{15}=3.14$

Report an Error

Example Question #372 : Basic Geometry

In the game of Sumo, both wrestlers are placed on the outer edge of the ring, on opposite sides of each other. If the wrestling ring is a perfect circle and has an area of $804.25\;ft^2$ , what would be the distance between both wrestlers?

Possible Answers:

$64\;ft$

$56\;ft$

$16\;ft$

$32\;ft$

$256\;ft$

Correct answer:

$32\;ft$

Explanation:

With the two wrestlers standing opposite each other on the edge of the ring, the distance between them would constitute the diameter of the circle. We can use the formula for circular area to find the diameter:

$\\area=\pi\cdot r^2\\ \\804.25\;ft^2=3.14159\cdot r^2\\ \\r^2=\frac{804.25\;ft^2}{3.14159}=256\;ft^2\\ \\radius=\sqrt{256\;ft^2}=16\;ft\\ \\diameter=2\cdot16\;ft=32\;ft$

Report an Error

Example Question #372 : Plane Geometry

True or false: A circle with radius 1 has circumference less than 4.

Possible Answers:

False

True

Correct answer:

False

Explanation:

The circumference of a circle is equal to its radius multiplied by $2 \pi$ , so, if the radius of a circle is 1, its circumference is

$1 \times 2 \pi = 2\pi \approx 2 \cdot 3.14 \approx 6.28$

This is greater than 4.

Report an Error

View Tutors

Robyn
Certified Tutor

Washington College, Bachelor of Science, Business Administration and Management.

View Tutors

Katherine
Certified Tutor

Utah State University, Bachelor of Science, Management Information Systems. University of Phoenix-Utah Campus, Masters in Bus...

View Tutors

Elvis
Certified Tutor

Methodist University, Bachelor of Science, Mathematics and Computer Science.

All Basic Geometry Resources

9 Diagnostic Tests 164 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

GMAT Tutors in Washington DC, Statistics Tutors in Atlanta, MCAT Tutors in Los Angeles, MCAT Tutors in Dallas Fort Worth, SAT Tutors in Phoenix, ISEE Tutors in Washington DC, Physics Tutors in New York City, Physics Tutors in Houston, GRE Tutors in Dallas Fort Worth, ACT Tutors in Phoenix

Popular Courses & Classes

GRE Courses & Classes in Phoenix, Spanish Courses & Classes in Boston, Spanish Courses & Classes in Denver, GRE Courses & Classes in Seattle, ISEE Courses & Classes in Washington DC, Spanish Courses & Classes in Miami, SAT Courses & Classes in Washington DC, SSAT Courses & Classes in Houston, SAT Courses & Classes in Seattle, MCAT Courses & Classes in Seattle

Popular Test Prep

ISEE Test Prep in Denver, GRE Test Prep in Dallas Fort Worth, SAT Test Prep in Seattle, ISEE Test Prep in Dallas Fort Worth, MCAT Test Prep in Los Angeles, MCAT Test Prep in Washington DC, SAT Test Prep in Washington DC, MCAT Test Prep in Atlanta, ISEE Test Prep in Miami, MCAT Test Prep in Chicago

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Basic Geometry : Plane Geometry

Study concepts, example questions & explanations for Basic Geometry

All Basic Geometry Resources

Example Questions

Example Question #371 : Basic Geometry

Example Question #372 : Basic Geometry

Example Question #1 : How To Find The Ratio Of Diameter And Circumference

Example Question #1 : How To Find The Ratio Of Diameter And Circumference

Example Question #371 : Basic Geometry

Example Question #2 : How To Find The Ratio Of Diameter And Circumference

Example Question #372 : Basic Geometry

Example Question #72 : Diameter

Example Question #372 : Basic Geometry

Example Question #372 : Plane Geometry

All Basic Geometry Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: