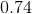Call Now to Set Up Tutoring:

(888) 888-0446

Basic Arithmetic : Basic Arithmetic

Study concepts, example questions & explanations for Basic Arithmetic

Create An Account

All Basic Arithmetic Resources

6 Diagnostic Tests 75 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #2 : Changing A Decimal To A Percent

What is 0.87 as a percent?

Possible Answers:

$87\%$

$870\%$

$0.87\%$

$8.7\%$

Correct answer:

$87\%$

Explanation:

To change a decimal into a percent, start by multiplying the decimal by 100.

$0.87\times100=87$

Then, add a percent sign to the end of that number.

$87\rightarrow87\%$

Report an Error

Example Question #3 : Changing A Decimal To A Percent

What is 0.71 as a percent?

Possible Answers:

$7.1\%$

$71\%$

$710\%$

$0.71\%$

Correct answer:

$71\%$

Explanation:

To change a decimal into a percent, start by multiplying the decimal by 100.

$0.71\times100=71$

Then add a percent sign to the end of the number.

$71\rightarrow71\%$

Report an Error

Example Question #5 : Changing View

What is 0.54 as a percent?

Possible Answers:

$540\%$

$0.54\%$

$5.4\%$

$54\%$

Correct answer:

$54\%$

Explanation:

To change a decimal into a percent, multiply the decimal by 100 then add the percent sign.

$0.54\times100=54$

$54\rightarrow 54\%$

Report an Error

Example Question #6 : Changing View

Change 0.99 into a percent.

Possible Answers:

$0.99\%$

$990\%$

$99\%$

$9.9\%$

Correct answer:

$99\%$

Explanation:

To change a decimal into a percent, multiply the decimal by 100 then add a percent sign at the end of that number.

$0.99\times100=99$

$99\rightarrow99\%$

Report an Error

Example Question #31 : Percents And Decimals

What is 0.95254 expressed as a percentage rounded to the nearest tenth?

Possible Answers:

$\small \small 0.95\%$

$\small 95.25\%$

$\small 100\%$

$\small \small 95\%$

$\small 95.3\%$

Correct answer:

$\small 95.3\%$

Explanation:

Percents are numbers expressing parts of $\small 100$ : $\small \small 1\%$ means $\small 1$ part of $\small 100$ , or $\small \frac{1}{100}$ .

The simplest way to convert a decimal to a percentage is to move the decimal place over two places to the right. We move the decimal point to after the hundredths place because we are rewriting the decimal as a portion of $\small 100$ . Therefore:

$\small 0.9525=95.25\%$

Now, we need to round the percentage to the nearest tenth. The number after the tenths place is a five, so we need to round up:

$\small 95.25\%\Rightarrow95.3\%$

$\small 95.3\%$ is therefore our final answer.

Report an Error

Example Question #8 : Changing View

What is $\small 2.420398$ expressed as a percentage rounded to the nearest hundredth?

Possible Answers:

$\small 242.04\%$

$\small 2.42\%$

$\small 24.20\%$

$\small 0.02\%$

$\small 242\%$

Correct answer:

$\small 242.04\%$

Explanation:

Percents are numbers expressing parts of $\small 100$ : $\small \small 84\%$ is the same thing as saying $\small 84$ parts of $\small 100$ or $\small \frac{84}{100}$

$\small 2.420398=242.0398\%$

In everyday usage, percents usually are between $\small \small 0\%$ and $\small 100\%$ . However, when a number is greater than $\small 1$ , it's corresponding percentage is going to be greater than $\small 100\%$ . The next step of this problem is to round the percentage we have to the nearest hundredth. The number in the thousandths place is $\small 9$ , therefore, we're going to round up:

$\small 242.0398\%\Rightarrow242.04\%$

$\small 242.04\%$ is therefore our final answer.

Report an Error

Example Question #7 : Changing View

Change $78\%$ to a decimal.

Possible Answers:

0.078

7.8

0.78

Correct answer:

0.78

Explanation:

To change a percent to a decimal, drop the "%" sign then divide by 100.

$78\%\rightarrow78$

$\frac{78}{100}=0.78$

Report an Error

Example Question #1 : Changing A Percent To A Decimal

What is $74\%$ as a decimal?

Possible Answers:

0.074

7.4

0.74

740.0

Correct answer:

0.74

Explanation:

To change a percent by the decimal, first drop the percent sign.

$74\%\rightarrow74$

Then, divide the number by 100.

$74\div100=0.74$

Report an Error

Example Question #32 : Percents And Decimals

Convert the following percent to a decimal:

$68\%$ .

Possible Answers:

0.068

6.8

0.608

0.68

Correct answer:

0.68

Explanation:

To convert a percent into a decimal, divide the percent by 100 or move the decimal point 2 places to the left.

$\frac{68}{100}=0.68$ or 68 hundredths.

Report an Error

Example Question #33 : Percents And Decimals

Convert the following percent to a decimal:

$1.33\%$ .

Possible Answers:

0.133

1.33

0.00133

0.0133

Correct answer:

0.0133

Explanation:

To convert a percent to a decimal, divide the percent by 100 or move the decimal point two places to the left.

$\frac{1.33}{100}=0.0133$

Report an Error

View Arithmetic Tutors

Melissa
Certified Tutor

University of Houston, Bachelors, Political Science and Government.

View Arithmetic Tutors

Irina
Certified Tutor

New York University, Bachelors, Biochemistry.

View Arithmetic Tutors

Rhonda
Certified Tutor

University of Louisville, Bachelors, Accounting. University of Louisville, Masters, Business Education/ Special Education.

All Basic Arithmetic Resources

6 Diagnostic Tests 75 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Computer Science Tutors in Washington DC, GMAT Tutors in Boston, Physics Tutors in Chicago, GRE Tutors in Boston, Spanish Tutors in Los Angeles, Reading Tutors in Washington DC, SAT Tutors in Dallas Fort Worth, Physics Tutors in Philadelphia, SAT Tutors in Philadelphia, GMAT Tutors in Seattle

Popular Courses & Classes

Spanish Courses & Classes in Washington DC, LSAT Courses & Classes in Miami, ACT Courses & Classes in Dallas Fort Worth, SSAT Courses & Classes in Philadelphia, MCAT Courses & Classes in San Francisco-Bay Area, Spanish Courses & Classes in San Diego, ISEE Courses & Classes in Miami, SSAT Courses & Classes in Phoenix, LSAT Courses & Classes in Seattle, MCAT Courses & Classes in Atlanta

Popular Test Prep

ACT Test Prep in Miami, SSAT Test Prep in Phoenix, ACT Test Prep in San Francisco-Bay Area, ACT Test Prep in Denver, MCAT Test Prep in Los Angeles, GRE Test Prep in San Francisco-Bay Area, LSAT Test Prep in Dallas Fort Worth, ISEE Test Prep in Denver, LSAT Test Prep in Boston, GRE Test Prep in Dallas Fort Worth

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Basic Arithmetic : Basic Arithmetic

Study concepts, example questions & explanations for Basic Arithmetic

All Basic Arithmetic Resources

Example Questions

Example Question #2 : Changing A Decimal To A Percent

Example Question #3 : Changing A Decimal To A Percent

Example Question #5 : Changing View

Example Question #6 : Changing View

Example Question #31 : Percents And Decimals

Example Question #8 : Changing View

Example Question #7 : Changing View

Example Question #1 : Changing A Percent To A Decimal

Example Question #32 : Percents And Decimals

Example Question #33 : Percents And Decimals

All Basic Arithmetic Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: