AP Statistics : Statistical Patterns and Random Phenomena
Study concepts, example questions & explanations for AP Statistics
All AP Statistics Resources
Example Questions
Example Question #81 : Statistical Patterns And Random Phenomena
Example Question #1 : How To Do The Linear Transformation Of A Random Variable
Variable 
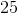
Because 
Therefore, since we are given the mean of 25, we can find its variance to also be 25.
Example Question #1 : How To Use Tables Of Normal Distribution
Find the area under the standard normal curve between Z=1.5 and Z=2.4.
0.3220
0.0822
0.9000
0.0768
.0586
.0586
Example Question #1 : Normal Distribution
Alex took a test in physics and scored a 35. The class average was 27 and the standard deviation was 5.
Noah took a chemistry test and scored an 82. The class average was 70 and the standard deviation was 8.
Show that Alex had the better performance by calculating -
1) Alex's standard normal percentile and
2) Noah's standard normal percentile
Alex = .778
Noah = .723
Alex = .901
Noah = .926
Alex = .945
Noah = .933
Alex = .855
Noah = .844
Alex = .923
Noah = .911
Alex = .945
Noah = .933
Alex -
Noah -
Example Question #2 : How To Use Tables Of Normal Distribution
When
and
Find
.68
.76
.81
.61
.72
.72
Example Question #2 : Normal Distribution
Arrivals to a bed and breakfast follow a Poisson process. The expected number of arrivals each week is 4. What is the probability that there are exactly 3 arrivals over the course of one week?
Example Question #1 : How To Use Tables Of Normal Distribution
The masses of tomatoes are normally distributed with a mean of 
The Z score for a normal distribution at the 
Example Question #2 : Normal Distribution
Find
First, we use our normal distribution table to find a p-value for a z-score greater than 0.50.
Our table tells us the probability is approximately,
Next we use our normal distribution table to find a p-value for a z-score greater than 1.23.
Our table tells us the probability is approximately,
We then subtract the probability of z being greater than 0.50 from the probability of z being less than 1.23 to give us our answer of,
Example Question #3 : Normal Distribution
Find
First, we use the table to look up a p-value for z > -1.22.
This gives us a p-value of,
Next, we use the table to look up a p-value for z > 1.59.
This gives us a p-value of,
Finally we subtract the probability of z being greater than -1.22 from the probability of z being less than 1.59 to arrive at our answer of,
Example Question #3 : Normal Distribution
Gabbie earned a score of 940 on a national achievement test. The mean test score was 850 with a sample standard deviation of 100. What proportion of students had a higher score than Gabbie? (Assume that test scores are normally distributed.)
When we get this type of problem, first we need to calculate a z-score that we can use in our table.
To do that, we use our z-score formula:
where,
Plugging into the equation we get:
We then use our table to look up a p-value for z > 0.9. Since we want to calculate the probability of students who earned a higher score than Gabbie we need to subtract the P(z<0.9) to get our answer.
Certified Tutor
All AP Statistics Resources
