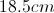All AP Physics C: Mechanics Resources
Example Questions
Example Question #181 : Ap Physics C

A nonuniformly charged ring of radius 

Use a polar coordinate system, the given linear charge density 


Example Question #21 : Electricity And Magnetism Exam

In this model of a dipole, two charges 






By the law of cosines, the distance from the point to charge 

The distance to charge 




Lastly, the exact potential is given by

Remark: Far from the dipole (approximating 

Example Question #22 : Electricity And Magnetism Exam

A uniformly charged hollow spherical shell of radius 



Use a spherical coordinate system and place the point of interest a distance 



.
Remarkably, this is the same potential that would exist a distance 
Example Question #31 : Electricity

A thin bar of length L lies in the xy plane and carries linear charge density 



Use the linear charge density 



Example Question #31 : Electricity

A uniformly charged ring of radius 


Use the linear charge density 





Example Question #11 : Calculating Electric Potential

A uniformly charged square frame of side length 

You may wish to use the integral:
Calculate the potential due to one side of the bar, and then multiply this by 


Example Question #181 : Ap Physics C
Consider a spherical shell with radius 

Zero
Zero
According to the shell theorem, the total electric field at the center point of a charged spherical shell is always zero. At this point, any electric field lines will result in symmetry, canceling each other out and creating a net field of zero at that point.
Example Question #1 : Interpreting Electric Charge Diagrams
A charge of unknown value is held in place far from other charges. Its electric field lines and some lines of electric equipotential (V1 and V2) are shown in the diagram.

A second point charge, known to be negative, is placed at point A in the diagram. In which direction will the second, negative charge freely move?
Toward point A
Toward point C
Toward the original charge Q
It will remain stationary
Toward point C
The original charge Q is negative, as indicated by the direction of the electric field lines in the diagram. A negative point charge of any value placed at point A will cause both charges to feel a mutually repelling force on each other. Therefore, the second charge will be repelled by the original negative charge with a force pointing radially along a line connecting the center of Q and the point A, resulting in free movement toward C. Additionally, point B is on a line of equipotential to point A; negative point charges will move from regions of lower electric potential to higher electric potential (against the direction of the electric field lines), so point B is not a viable answer.
Example Question #1 : Understanding Magnetic Fields And Charges
A proton traveling 


To calculate the magnetic force of a single charge, we use 



Since this magnetic force causes the proton to travel in a circular path, we set this magnetic force equation equal to the centripetal force equation.



Using the values given in the question, we can solve for the radius.
Example Question #32 : Electricity And Magnetism Exam
Which of the following best describes the net magnetic flux through a closed sphere, in the presence of a magnet?
Negative only if the north pole of the magnet is within the surface
Zero only if the magnet is completely enclosed within the surface
Positive only if the north pole of the magnet is within the surface
Zero regardless of the orientation of the magnet
More than one of the other options is true
Zero regardless of the orientation of the magnet
The net magnetic flux (or net field flowing in and out) through any closed surface must always be zero. This is because magnetic field lines have no starting or ending points, so any field line going into the surface must also come out. In other words, "there are no magnetic monopoles."
All AP Physics C: Mechanics Resources









![=\frac{b}{4\pi\epsilon_0}\left [\frac{\theta}{2}-\frac{\sin2\theta}{4} \right ]_{0}^{2\pi}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/891167/gif.latex)













![=\frac{1}{4\pi\epsilon_0} \left (\frac{Q}{2} \right ) \left [\frac{1}{Ra}\sqrt{R^2 + a^2-2Ra\cos\theta} \right ]_{0}^{\pi}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/890844/gif.latex)









![= \frac{b}{4\pi\epsilon_0}\left [ \sqrt{x^2+a^2}\right ]_{0}^{L}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/891578/gif.latex)









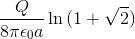






![=\frac{Q}{4\pi\epsilon_{0}a}\left[ \ln\left (\sqrt{x^2+\frac{a^2}{4}} +x\right )\right]_{-a/2}^{a/2}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/891564/gif.latex)