All AP Physics C: Mechanics Resources
Example Questions
Example Question #151 : Mechanics Exam
Two identical atoms, A and B, are at rest some distance apart in a vacuum.
If atom A moves at a constant velocity, 
Atom A moves with velocity 
The velocity of atom A is 
The velocity of atom B after the collision is
The velocities of the identical atoms are the same, but in opposite directions after the collision
The speed of both atoms is the same after collision
The velocity of atom A is 
Assuming the atoms have the same mass, a collision between atoms in a vacuum is most nearly an elastic collision. This means the kinetic energy of the system is conserved and when they collide, all of the kinetic energy in atom A will be transferred perfectly to atom B. So just after collision, atom A will have velocity 

Example Question #152 : Ap Physics C
A pickup truck with a mass of 

It turns out the truck can only take on an additional 

The equation for conservation of momentum is:
Given:
Plug in given values into the conservation of momentum equation.
Simplify.
Subtract the final velocity from the initial velocity to find change in speed (since these velocities are in the same direction).

Example Question #153 : Ap Physics C
A pickup truck with a mass of 

Assuming no outside forces are acting on the system, how many 

Because of conservation of momentum, the product of the initial mass and velocity should equal the final mass and velocity. The equation for conservation of momentum is:
The initial mass of the truck is
The initial velocty is
The final velocity is 
Plug in known values to the conservation of momentum equation.
Simplify.
Note that while necessary, the final mass is not our final answer. The final mass, 


The mass of the truck is known so set up an equation and solve for the mass of sand added to the truck.
Example Question #1 : Electricity And Magnetism Exam
A hollow metal sphere with a diameter of 10cm has a net charge of 

Relevant equations:

Anywhere outside the metal sphere, the electric field is the same as it would be for a point charge of the same magnitude, located at the center of the sphere. So, calculate the electric field of a point charge given:
Plugging in gives:
Example Question #2 : Electricity And Magnetism Exam
Two infinite parallel conducting sheets each have positive charge density 





Relevant equations:

Electric field is additive; in other words, the total electric field from the two planes is the sum of their individual fields:
The direction of the electric field is away from positive source charges. Thus, to the right of these positively charged planes, the field points away to the right.
Example Question #1 : Electricity And Magnetism Exam
Four particles, each of charge 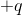


Directly to the right
Directly to the left
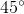

The correct answer is 45 degrees upwards of left. Since all particles have charge 

Example Question #3 : Electricity And Magnetism Exam
Consider a spherical capacitor made of two nested spheres. The smaller sphere has a radius of 



Which of the following equations accurately describes the capacitance of this spherical capacitor?
Due to symmetry, this scenario would not produce capacitance
To solve this problem, we will need to derive an equation.
We know that:
We can use Gauss's law to derive the electric field between the two circles yielding:
Doing our integration with respect to 


We can plug this back into our equation for capacitance to get:
Example Question #1 : Electricity
We have a point charge of 

Coulomb's law for the electric field from point charges is 
Using these values, we can solve for the electric field.
Example Question #4 : Electricity And Magnetism Exam
Two positive point charges of 





To find the location at which the test charge experience zero net force, write the net force equation as 




In this equation, the distance, 




Cross-multiply.
We can cancel 

Now that we have isolated 
Example Question #5 : Electricity And Magnetism Exam
You are standing on top of a very large positively charged metal plate with a surface charge of .
Assuming that the plate is infinitely large and your mass is 
Consider the forces that are acting on you. There is the downward (negative direction) force of gravity, . In order for you to float, there has to be an upward (positive direction) force, and that upward force is coming from the metal plate,
. To show that you would float, the net force equation is written as


For plates that are charged, know that 
Knowing this, the force equation becomes 
Solve for 
Now we can plug in our given values, and solve for the charge.
All AP Physics C: Mechanics Resources






























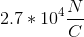

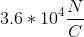
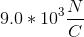





















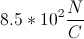
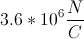












%5E2=kq_2qr%5E2)





















