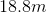Since half of the log is floating above the water, the buoyant force must equal the gravitational force on the log for the net force to equal .

When the ball is stably submerged (no longer accelerating), the buoyant force will equal the gravitational force.

Let the mass of the ball be .

The buoyancy force is equal to the weight of the material the ball displaces, which is .

 is the volume of the material the ball displaces.

We need the mass of the ball in terms of its density, which is .

From equation ,

Solving for  we get

.

This is the entire volume of the ball, so the whole ball is submerged. 

Here is a more complicated route to the solution that would be necessary if the density of the water was greater than the ball:

Using the geometry of a spherical cap, you'll find the volume as a function of the depth  is . Setting this equal to volume displaced we get

In order for these to equal

This can also be done conceptually by realizing in order for the buoyant force to equal the gravitation force, the whole ball must be submerged since the density of the ball and water are equivalent. 

Note*: Any answer greater than  would also be acceptable since the ball would still be completely submerged, and the buoyancy force would still equal the gravitation force. However, the only answer choice greater than or equal to  is , so that is the answer.

In this question, we're told that three balls of differing densities are submerged in water. We're then asked to determine the relative rates at which the balls will rise to the surface.

To begin, it's important to realize that whenever an object is submerged under water, there are two main forces acting upon it. One of these is the gravitational force, which points downwards. The other main force is the buoyant force, which acts upwards on the object. Because these two forces act in opposite directions, they can either cancel each other out partially or even completely.

Ball A, which has a density greater than water's, will not float to the surface but will rather sink to the bottom. This is because the gravitational force of ball A will be greater than the buoyant force from the displaced water. Consequently, there will be a net force downward.

For balls B and C, both of them have a density less than water. Hence, each of them will experience a net upward force and will thus rise to the surface. However, the magnitude of the upward force that each experiences will be different. This net upward force will, in turn, influence the degree to which each ball accelerates and will thus affect the rate at which they rise to the surface.

Ball B has a greater density than ball C. As a result, its gravitational force constitutes a greater downward force compared to ball C. The significance of this is that the net upward force for ball B will be lower than that of ball C. Thus, ball C will rise to the surface faster than ball B because it is enacted on by a greater net upward force.

So all in all, ball B and C will both float to the top. Ball C will reach the surface faster than ball B. Ball A, however, will sink to the bottom.

We can begin this problem by writing the equation for pressure.

We have to remember that the value of atmospheric pressure is equal to 1atm, which is also equal to 101325Pa.

Now, if we set the gauge pressure equal to three times the atmospheric pressure, we can solve for the depth.

The cube has a volume of . It is necessary to know the sidelength of the cube to know the height of the cube.

Use the pressure formula.

Rewrite the equation to solve for (rho density of the fluid) then plug in known values.

This is approximately 

Pressure increases with depth according to:

Since the pressure at the surface of the ocean is the same as the pressure inside the bathysphere, we can ignore both. (This is called gauge pressure, or pressure above one atmosphere). Find the pressure at our depth:

Find the area of the hatch, and use the definition that force is pressure times area:

The interface between the liquids occurs at the bottom of the tube. Here, the pressure is the same. We also know that the tube is open to atmospheric pressure at the top of each side of the tube. Thus, we can create two equations for the pressure at the interface and set them equal to each other: 


By setting these equal to one another the result is: 
 
Since the density of water is greater than that of oil, we can conclude that the height of the oil column will be greater than that of the water. 

The pressure in a tire is a gauge pressure; the 25psi is the difference between the pressure in the tire and atmospheric pressure, and does not add atmospheric pressure to reach the measured number. Absolute pressure adds these quantities together. 

The pressure at the lake's surface is just the atmospheric pressure, . The pressure at depth  below the surface is . Therefore, the pressure difference is given as .

We can then substitute the values in to arrive at the answer in :

Recall that this pressure is known as gauge pressure, and that the total pressure at the point underwater in the lake includes gauge pressure and atmospheric pressure.

This question is presenting us with a situation in which an object (a person) submerged in a liquid is experiencing pressure. To solve for the correct pressure, we'll need to take a few things into account.

First, we'll need to consider the density of the liquid. In this case, we're told that the liquid is saltwater, and we're given the density in the question stem. Second, we'll need to consider how far below the surface of the liquid our object is. Again, this value is given to us in the question stem. And third, we also need to remember that there is a pressure above the liquid, which is the pressure coming from the atmosphere. This value (which should be committed to memory) is , or .

Putting all these considerations together, we have an equation that we can use to calculate the pressure.

Plug in the values that we know and solve for total pressure.