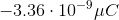The elemental charge is the magnitude of charge, in Coulombs, that each electron or proton has. Because electrons have a negative charge, don't forget to add a negative sign into the equation.

When you convert the answer to microcoulombs, the answer is :

The equation for the quantity of charge is:

where  is the charge quantity,  represents the number of electrons, and  is the charge of an electron, also known as the elementary charge.

Rewrite the equation.

One coulomb, , consists of electrons,

Substitute these two values into the formula.

This number represents the electron's fundamental charge. 

Because this is a neutral balloon, the net charge is equal to the charge the was removed, but opposite in sign. There were 16,000 electrons removed, each of which has a charge of . Therefore, the total charge that was                       removed is:

To answer the question, we must remember that if that much charge was removed from the balloon, the balloon will now be negative.

Surface area of sphere:

Plug in values:

A way to think of flux is to count the number of electric field lines exiting a shape and subtract from it the number of field lines entering the shape. The only way for there to be more lines exiting the shape than entering the shape (and the only way to have any flux) is when the shape is enclosing charge.

In our problem, the box has no charge in it. Therefore, it has the same amount of field lines leaving it as it does entering it. This means that there is 0 net flux through the box. 

Because the box is a conductor, the electrons are able to shift when charge is applied. Because the box is isolated, there is nothing else exerting influence over the box.

The electrons on the shell are able to move from the electric field made by , so they group together on the inner surface of the box to make a net charge of . Because  worth of electrons moved from the outer surface, the outer surface necessarily has a net charge of  now, because it was neutral before.

A superconductor is a material that has 0 electrical resistance when cooled to below a certain temperature.

In general, materials have a decreasing resistance as they are cooled. With a superconductor, once the critical temperature is reached, the resistance abruptly goes to 0. Superconductivity is a quantum mechanical phenomenon.

We are told that there is an electric field pointing vertically down and that the positive end is near the top. If a charged particle were placed in this field, it will experience an upward electric force, while its mass would cause it to experience a downward gravitational force. We are looking for a situation in which these two forces are equal in order for the particle to be in static equilibrium, thus we need to set the gravitational force equal to the electric force.

To calculate the net charge of the system, it is necessary to know the charge of an electron.  Write the charge of an electron.

Multiply this number by the existing number of electrons in the systems.

For this question, we need to figure out the voltage difference between two points. We're provided with the charge of the particle, the amount of energy put into the process, and the distance traversed by the particle.

First, let's write an equation for voltage.

Where  is electrical potential energy, and  is the charge of the particle.

This equation describes the change in potential energy that occurs when a given quantity of charge undergoes a displacement while within an electric field. Since we are putting energy into this process to make it occur, and the charge is positive, we know that the voltage change will also be positive; that is, the positively charged particle will move towards the positive terminal of a voltage source and away from the negative terminal.

Plugging in the values given to us, we obtain:

Notice that we did not need to know the distance that the particle traveled in this case; that information is extraneous.