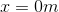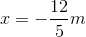All AP Physics 2 Resources
Example Questions
Example Question #1 : Point Charges
You have two charges on an axis. One charge of 

There is no point on the axis at which the electric field is 0
The equation for an electric field from a point charge is
To find the point where the electric field is 0, we set the equations for both charges equal to each other, because that's where they'll cancel each other out. Let 


Therefore, the only point where the electric field is zero is at 
Example Question #2 : Point Charges
A charge of 



To find where the electric field is 0, we take the electric field for each point charge and set them equal to each other, because that's when they'll cancel each other out.
The 
Therefore, the electric field is 0 at 
Example Question #1 : Electrostatics
Imagine two point charges 2m away from each other in a vacuum. One of the charges has a strength of 
There is not enough information to determine the strength of the other charge
The equation for force experienced by two point charges is
We're trying to find 
Now, we can plug in our numbers.
Therefore, the strength of the second charge is 
Example Question #1 : Electrostatics

What is the electric force between these two point charges?
The force between two point charges is shown in the formula below:





Plugging in the numbers into this equation gives us
Example Question #3 : Point Charges

Suppose there is a frame containing an electric field that lies flat on a table, as is shown. A positively charged particle with charge 




We are given a situation in which we have a frame containing an electric field lying flat on its side. In this frame, a positively charged particle is traveling through an electric field that is oriented such that the positively charged terminal is on the opposite side of where the particle starts from. We are being asked to find the horizontal distance that this particle will travel while in the electric field. Since this frame is lying on its side, the orientation of the electric field is perpendicular to gravity. Therefore, the only force we need concern ourselves with in this situation is the electric force - we can neglect gravity. However, it's useful if we consider the positive y-direction as going towards the positive terminal, and the negative y-direction as going towards the negative terminal. It's also important to realize that any acceleration that is occurring only happens in the y-direction. That is to say, there is no acceleration in the x-direction. We'll start by using the following equation:
We'll need to find the x-component of velocity.
Our next challenge is to find an expression for the time variable. To do this, we'll need to consider the motion of the particle in the y-direction. Also, since the acceleration in the y-direction is constant (due to a constant electric field), we can utilize the kinematic equations.
And since the displacement in the y-direction won't change, we can set it equal to zero.
Just as we did for the x-direction, we'll need to consider the y-component velocity.
We also need to find an alternative expression for the acceleration term. We can do this by noting that the electric force is providing the acceleration.
Also, it's important to remember our sign conventions. Since the electric field is pointing from the positive terminal (positive y-direction) to the negative terminal (which we defined as the negative y-direction) the electric field is negative.
Now, plug this expression into the above kinematic equation.
Rearrange and solve for time.
Now that we've found an expression for time, we can at last plug this value into our expression for horizontal distance.
And lastly, use the trigonometric identity:
Example Question #3 : Point Charges

Suppose there is a frame containing an electric field that lies flat on a table, as shown. A positively charged particle with charge 




We are given a situation in which we have a frame containing an electric field lying flat on its side. In this frame, a positively charged particle is traveling through an electric field that is oriented such that the positively charged terminal is on the opposite side of where the particle starts from. We are being asked to find an expression for the amount of time that the particle remains in this field. Since this frame is lying on its side, the orientation of the electric field is perpendicular to gravity. Therefore, the only force we need concern ourselves with in this situation is the electric force - we can neglect gravity. However, it's useful if we consider the positive y-direction as going towards the positive terminal, and the negative y-direction as going towards the negative terminal. To begin with, we'll need an expression for the y-component of the particle's velocity.
Next, we'll need to make use of one of the kinematic equations (we can do this because acceleration is constant).
Since the particle will not experience a change in its y-position, we can set the displacement in the y-direction equal to zero.
At this point, we need to find an expression for the acceleration term in the above equation. The only force on the particle during its journey is the electric force.
It's also important for us to remember sign conventions, as was mentioned above. Since the electric field is pointing towards the negative terminal (negative y-direction) is will be assigned a negative value.
Now, plug this expression for acceleration into the previous expression we derived from the kinematic equation, we find:
Cancel negatives and expand the expression for the y-component of velocity, so we are left with:
Rearrange to solve for time.
Example Question #61 : Electricity And Magnetism
An object of mass 


Combine Newton's second law with the equation for electric force due to an electric field:
Plug in values:
Example Question #1 : Point Charges
At 

None of these
Since the electric field is pointing towards the charge, it is known that the charge has a negative value.
Using electric field formula:
Solving for
Plugging in values:
Since the charge must have a negative value:
Example Question #9 : Point Charges
Imagine two point charges separated by 5 meters. One has a charge of 

Attractive
There is no force felt by the two charges.
Attractive
Repulsive
Repulsive
Attractive
The equation for the force experienced by two point charges is known as Coulomb's Law, and is as follows.
The value 'k' is known as Coulomb's constant, and has a value of approximately 
We have all of the numbers necessary to use this equation, so we can just plug them in.
Since we're given a negative number (and through our intuition: "opposites attract"), we can determine that the force is attractive. Because we're asked for the magnitude of the force, we take the absolute value, so our answer is

Example Question #61 : Electricity And Magnetism
What is the value of the electric field 3 meters away from a point charge with a strength of 
None of the answers are correct.
To find the strength of an electric field generated from a point charge, you apply the following equation.
We know the value of Q and r (the charge and distance, respectively), so we can simply plug in the numbers we have to find the answer.
While this might seem like a very large number coming from such a small charge, remember that the typical charges interacting with it will be in the same magnitude of strength, roughly. This yields a force much smaller than 10,000 Newtons.
Certified Tutor
All AP Physics 2 Resources