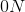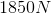Diffraction is the bending of light around an object. It is seen in the Double Slit experiment in which waves are spread out from their initial line of travel.

The buoyant force on the ball is simply the weight of water displaced by the ball:

The force of gravity on the ball is:

These forces oppose each other, so we can say:

The net force on the ball is expressed as:

Since it is accelerating downward, we know that the force of gravity is stronger than the buoyant force, so we can write:

Substitute expressions for each variable:

Rearrange to solve for the volume of the ball:

To answer this question, we'll need to make use of the concept of buoyancy and apply the following equation:

Also, remember that in this equation, the density and volume are that of the fluid that is displaced, not that of the object!

Since we are told that the object has a mass of 300g and is initially floating, we can set the buoyant force equal to the weight of the object.

It's important to realize that the volume of the fluid displaced is going to be equal to that portion of the object's volume that is submerged underwater. Since we're told that the object is cylindrical, and that 4cm of its height is under water, we can set up the following relationship:

Where  = Area of the cylinder and  = height of cylinder underwater

Plugging this value into the above equation and canceling common units on both sides, we obtain:

Now that we have found the area, we can calculate the mass that needs to be added to the cylinder in order to make it sink. To do this, we need to consider the scenario in which the cyclinder is completely submerged in the water the instant before it is about to sink. In this case, we're able to calculate the mass that needs to be added to the cylinder to make this happen.

Where  = the mass of mercury added to the cylinder

Thus far, we have determined that 450g of mercury needs to be added. Now, we just need to use the density of mercury in order to determine the volume needed.

Since the water is exerting an upward force  on the metal sample, it is receiving a force of equal magnitude pointing downward by Newton's third law. This downward force is transmitted by increased pressure in the water to the beaker and then to the scale.

The minimum size of the ballon will exert a buoyant force exactly equal to the gravitational force:

Now we have to be careful.  The mass is not just the mass of the man, but it includes the mass of the helium, as well. Canceling the 's and using subscripts to be careful:

The mass of the helium is its density times its volume:

Rearrange and solve for :

The buoyant force is the weight of the volume of water displaced by the immersed object. Since the rock is completely submerged, the buoyant force is the weight of water with the same volume as the rock. Despite the rock sinking, there is still a buoyant force; it is just less than the weight of the rock. 

Buoyant forces can be thought of as the force caused by displacing the amount of water that was previously there. The buoyant force is the weight of the volume of the liquid displaced by the object. Since the two masses have the same diameter, they have the same volume and thus, the same buoyant force. 

The weight of the object is . If the scale reads , this tells us that the buoyancy force has a magnitude of . Mathematically:

We may relate these parameters by Archimedes' principle:

This allows us to solve for the volume of the sphere, and thus, the radius of the sphere.

Now we may use the formula for volume of a sphere to solve for the radius:

In this question, we're told that two identical objects are submerged in water. The only thing that differs between them is the distance under the surface of water at which they're submerged. We're then asked to determine how this affects the buoyant force that each one experiences.

To answer this, we'll need to remember the expression for buoyant force.

The above expression tells us that the magnitude of the buoyant force is proportional to the density of the water or fluid, the volume of the water displaced, and the acceleration due to gravity.

It's important to also realize that no where in this expression does it say that the buoyant force is related to the depth of the object. Therefore, because the two objects are the same, and because they're both fully submerged, they will both be displacing the same volume of water. Consequently, the buoyant force on each is the same.