All AP Physics 1 Resources
Example Questions
Example Question #871 : Newtonian Mechanics
A book exerts a force of 2N downwards, into a chair that exerts a force of 5N dowwards to the floor it stands on. What is the force that the floor exerts upwards on the chair?
By Newton's third law, for every reaction there is an equal and opposite reaction. The floor must exert a 7N force upwards on the chair for the system to remain at rest. If it exerted less than that, the chair would be accelerating into the floor. This force, exerted by a surface, perpendicular to it, is called the normal force.
Example Question #4 : Newton's Third Law
A football player, feeling aggressive, is picking on a kid much smaller than himself. The football player asserts: "All of my hours in the weight room prove I can hit you harder than you hit me!" The smaller and more reserved gentleman replies: "Ya of course you can. I'm much weaker than you". Assuming by "hit" they mean "apply a force", are these two correct to think the football player can hit harder? Why?
Yes, Newton's second law says that football-playing-high-school bullies always hit harder.
No, Newton's third law says that the force two objects act on each other is always EQUAL in magnitude and opposite in direction.
Yes, Newton's second law says that the football player will cause the smaller gentleman to accelerate to a greater extent. Therefor he exterts a greater force.
No, Newton's first law says that the force two objects act on each other is always EQUAL in magnitude and opposite in direction.
No, Newton's third law says that the force two objects act on each other is always EQUAL in magnitude and opposite in direction.
The relative mass of two interacting objects does not influence the magnitude of the force that the two objects exert on each other. Newton's third laws states the force must be equal in magnitude. If you're trying to reconcile how a football player is unable to "hit harder" than someone who does not lift weights, the answer lies in Newton's second law.
The football player weighs more and thus experiences a small acceleration. The smaller gentleman experiences a large acceleration due to his relatively small mass. This large acceleration is what we view when we see a large football player hit someone smaller. The football player hardly changes his motion while the smaller person will fly backwards.
Example Question #1 : Newton's Third Law
Describe the phenomenon of a seat belt keeping someone restrained in their seat during a car crash. In other words, why did the person not leave their seat?
Newton's second law
Newton's first law
Tension force law
Newton's third law
All the laws describe why the person was not ejected from their seat
Newton's third law
While all three laws come into play in a car crash only one is specifically responsible for keeping a person restrained in their seat. Just before the crash, the passenger is moving along at the same speed as the car. When the car collides into the other car and decelerates, the person's body continues to move forward. This is Newton's first law, or the law of inertia. But it is Newton's third law that keeps the person from being ejected from their seat. The force of the person's body moving forward was matched by that of the seatbelt. For every action there is an equal and opposite reaction. If the seat belt was unable to "match" the force of the person's body moving forward against it, it would have snapped and the person would have continued forward.
Example Question #1 : Newton's Third Law
A locomotive is pushing a train at a constant velocity of 
They are the same in both magnitude and direction
None of these
They are the same in magnitude and opposite in direction
They are in opposite directions and have different magnitudes
They are in the same direction and have the same magnitude
They are the same in magnitude and opposite in direction
This is Newtons's third law. Every action has an equal an opposite reaction. The reason the train is able to move at all is due to the force the locomotive puts on the rails, which enables it to accelerate the cars.
Example Question #871 : Newtonian Mechanics
Two objects apply forces to each other. The force on one of the blocks as a function of time in the x-direction is 


By Newton's third law, every action has an equal and opposite reaction. So the force has an equal and opposite force on the other block. Mathematically, this just means to negate the force.
Example Question #11 : Newton's Third Law
Two men are having a shoving contest, each man pushes the other at the exact same time. Ross pushes Jake with 

The correct answer is 
Example Question #81 : Fundamentals Of Force And Newton's Laws
Consider the following system:
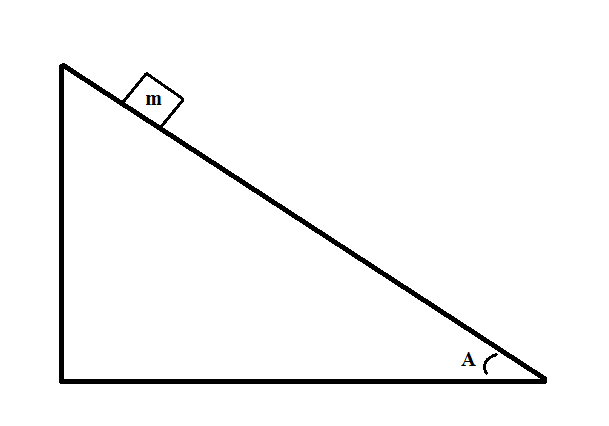
If the mass accelerates down the plane at a rate of 

Before we start using equations, we need to determine what forces are acting on the block in this system. The only relevant forces in this situation are gravity and friction. We are given the acceleration of the block, giving us the tools to find the net force.
Using Newton's second law, we can write:
The force of friction is subtracted because it is in the opposite direction of the movement of the block. Substituting in expressions for each variable, we get:
Canceling out mass and rearranging for the coefficient of kinetic friction, we get:
We have values for each variable, allowing us to solve:
Example Question #82 : Fundamentals Of Force And Newton's Laws
Consider the following system:

This system is set on a different planet, which has a gravitational constant different from that on Earth. If the angle measures 


There are two relevant forces acting on the block in this scenario: gravity and friction. We can use Newton's second law to solve this problem:
Substituting in expressions for each force, we get:
Eliminating mass and rearranging for 
At this point, we can plug in values for each variable and solve:
Example Question #1 : Force Diagrams

In the diagram, a massless string connects two blocks of mass 30 kg and 50 kg that are on a flat, frictionaless surface. A force 

Start by drawing in the forces acting on each block. You could also draw in the force of gravity and the normal force for each block, but they have been omitted from the image because they cancel each other out for each block and because there is no friction in this problem.

We are given in the question that the force 
In this problem, the two tension forces form an action/reaction pair and therefore are equal in magnitude but opposite in direction (Newton's third law). So:
We can solve for acceleration, since the tensions cancel out.
Now that we have acceleration, we need to write a new equation in which the tension force does not cancel out so that we can solve for the tension 
Do this by using Newton's second law again, except for only one of the blocks:
Lets consider the 30 kg block. The only force acting on the 30 kg block is the tension 
Example Question #2 : Force Diagrams
A ball with mass 

Find the magnitude of the ball's normal force.
The normal force is perpendicular to the plane:

First, we need to find 
We can solve for 



Rearranging to solve this equation for 
Substituting in the side lengths of the given triangle, we can solve for 
Note that the normal force is one of the legs of another right triangle. The other leg is the parallel force, and the hypotenuse is the force of gravity.
Using trigonometry, we know that
because 

Substituting in the known values into this equation, we can solve for the normal force:
All AP Physics 1 Resources






























































