All AP Physics 1 Resources
Example Questions
Example Question #325 : Linear Motion And Momentum
For a school exercise, students are tasked with determining an experimental value for Earth's gravitational acceleration. They decide to drop a ball and measure the time it takes until it hits the ground.
Which further measurements do the students need to take to determine an experimental value for Earth's gravitational acceleration without taking extraneous measurements?
The velocity of the ball just before it hits the ground.
Only the mass of the ball.
Only the height above the ground from which the ball is dropped.
The mass of the ball and the height from which the ball is dropped.
No further measurements are necessary.
Only the height above the ground from which the ball is dropped.
With only the drop height and the time we can use the kinematic equation:
We assume the initial velocity is 



Example Question #326 : Linear Motion And Momentum
A feather is released from rest on a moon with no atmosphere. The object drops 
What is the magnitude of the acceleration due to gravity on this moon?
We use the kinematic equation:
Plugging in 





Example Question #327 : Linear Motion And Momentum
A penny is dropped from the top of the Eiffel Tower. After falling uninterrupted for 

Assuming a constant gravitational acceleration, how far below the top of the Eiffel Tower is the penny after falling for a total of 
In the kinematic equation:
When the first term right of the equals sign goes to zero because the penny was dropped from rest, we see that the distance in a constant acceleration 

because the fraction and acceleration are constant.
So when 




Example Question #601 : Ap Physics 1
A bullet is fired horizontally simultaneously with a ball being dropped from the same height.
Assuming uninterrupted paths for both objects, how do the times it takes them to hit the ground compare?
There is not enough information to tell.
The ball hits the ground first.
The bullet hits the ground first.
The times for both objects to hit the ground are equal.
The ball hits the ground in half the time it takes the bullet to hit the ground.
The times for both objects to hit the ground are equal.
Horizontal velocity does not affect gravity's force on an object so both the bullet and the ball are accelerated downward at the same gravitational acceleration and they will hit the ground at the same time.
Example Question #602 : Ap Physics 1
In the traditional coordinate system, a car is speeding up while moving to the left.
What is the sign of the car's velocity?
Positive
It's impossible to tell.
Negative
It depends.
Neutral
Negative
In a traditional coordinate system: left and down are considered negative directions while up and right are considered positive directions. The question states that the object is moving to the left, so regardless of its acceleration, its velocity is negative at the time described.
Example Question #321 : Linear Motion And Momentum
John and Dave would like to meet at a coffee shop at the same time, John drives at 


So for this first we have to set up a relation between John (1) and Dave's (2) position. Keeping in mind that Dave is traveling the opposite distance of John.
Where x is the total distance between the two points. Then we solve it for time and plug it in to John's speed to find his distance after the elapsed time.
where 
Example Question #1 : Normal Force And Weight
A block of iron with mass 10kg is sitting on an incline that has an angle of 30 degrees above horizontal. What is the normal force on the block of iron?
The free body diagram of the system is shown below:


Since 

If you're confused as why it's cosine and not sine, think about the system practically. The flatter the slope is, the greater the normal force. The smaller an angle becomes (creating a flatter slope), the greater the value of cosine becomes, and subsequently the greater the normal force becomes.
Now we can simply plug in our given values:
Example Question #1 : Specific Forces
A person tries to lift a very heavy 

First, calculate the gravitational force acting on the rock.
The exerts a force of 



Example Question #2 : Forces
Consider the following system:
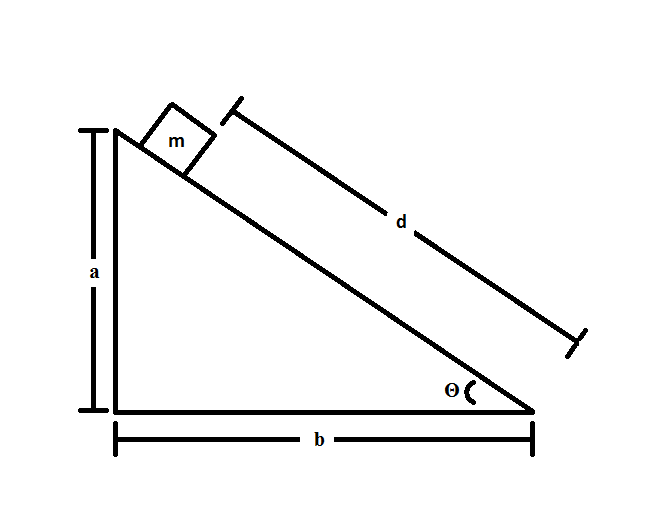
If the block is accelerating down the slope at an angle of 

There are two forces in play for this scenario: the first is gravity and the second is friction. We can use Newton's second law to solve this problem:
Substituing in the two forces we just mentioned:
Note that the force of friction is subtracted because it is in the opposite direction of the force of gravity. Now, substituting in expressions for our two forces, we get:
If you are unsure of whether to use cosine or sine for each force, think about the situation practically. The flatter the slope gets, the less the force of gravity will have an effect on moving the block down the plane, hence the use of the sine function. Also, the flatter the slope gets, the greater the normal force will become, hence the use of the cosine function.
Canceling out mass from the equation and rearranging to solve for the coefficient of friction, we get:
Example Question #2 : Normal Force And Weight
Consider the following system:

If the block travels down the slope at a constant speed and the coefficient of kinetic friction is 
There are two forces in play in this scenario. The first is gravity and the second is friction. Both depend on the angle of the slope. Since the block is traveling at a constant rate, we know the the gravitational and frictional force in the direction of the slope cancel each other out, and the net force is zero (there is no acceleration). Therefore, we can write:
Substituting in expressions for each force, we get:
If you are unsure of whether to use cosine or sine for each force, think about the situation practically. The flatter the slope gets, the less the force of gravity will have an effect on moving the block down the plane, hence the use of the sine function. Also, the flatter the slope gets, the greater the normal force will become, hence the use of the cosine function.
Canceling out mass and solving for the angle on one side of the equation, we get:
This is an important property to know! When an object travels down a slope at a constant rate, the tangent of the angle of the slope is equal to the coefficient of kinetic friction.
Certified Tutor
All AP Physics 1 Resources






































































