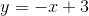All AP Calculus AB Resources
Example Questions
Example Question #1 : Ap Calculus Ab
Differentiate,

Differentiate,
Strategy
This one at first glance appears difficult even if we recognize that the chain rule is needed; we have a function within a function within a function within a function. To avoid making mistakes, it's best to start by defining variables to make the calculation easier to follow.
Let's start with the outermost function, we will write 

______________________________________________________
_______________________________________________________
Similarly, define 



_______________________________________________________
Write 
_______________________________________________________
Finally, define the inner-most function, 
________________________________________________________
Since 
That was easy enough, now just write everything in terms of 



Example Question #1 : Derivatives
Find the tangent line. Given the point (1,2)

To find the tangent line at the given point, we need to first take the derivative of the given function.
Power Rule:
Power rule says that we take the exponent of the “x” value and bring it to the front. Then we subtract one from the exponent.
Therefore, 
From there we plug in the "1" from the point to get our m value of the equation 

Therefore, the tangent line is equal to
Example Question #1 : Derivatives
Find the line tangent at the point (0,1)
To find the tangent line at the given point, we need to first take the derivative of the given function. The rule for functions with "e" in it says that the derivative of 
To put this into equation it will look like
From there we plug in the "0" from the point to get our m value of the equation . When we plug in "0" to y' we get m=3. Then from there, we will plug our point into 

Example Question #4 : Derivatives
Find the tangent line given the point (2,4) and the equation
To find the tangent line at the given point, we need to first take the derivative of the given function using Power Rule
Power rule says that we take the exponent of the “x” value and bring it to the front. Then we subtract one from the exponent.
From there we plug in the "2" from the point to get our m value of the equation . When we plug in "2" to y' we get m=8. Then from there, we will plug our point into now that we have found m to find our b value. So,
Plug this back into
Example Question #5 : Derivatives
Find the equation of the line tangent to the curve at the point where
Find the equation of the line tangent to the curve 

The slope of the line tangent at the given point will be equal to the derivative of 
Evaluate the secant term:
Therefore slope of the tangent line is simply:
So now we know the slope of the tangent line and can write the equation then solve for 
In order to solve for 
We now have our point:
Use the point to find
Example Question #6 : Derivatives
Find the slope of the line tangent to the curve of d(g) when g=6.
Find the slope of the line tangent to the curve of d(g) when g=6.
All we need here is the power rule. This states that to find the derivative of a polynomial, simply subtract 1 from each exponent and then multiply each term by their original exponent.
Constant terms will drop out when we do this, and linear terms will become constants.
From here substitute in g=6.
Example Question #1 : Derivative At A Point
Give the equation of the line tangent to the graph of the equation
at the point 
The tangent line to the graph of 



Apply the sum rule:
The tangent line is therefore the line with slope 5 through 
Example Question #1 : Derivatives
Give the equation of the line tangent to the graph of the equation
at the point 
None of the other choices gives the correct response.
None of the other choices gives the correct response.
The tangent line to the graph of 



Apply the constant multiple and sum rules:
Set 

Substituting back:
Evaluate 
The tangent line is therefore the line with slope 




This is not among the choices given.
Example Question #1 : Derivatives
Find the equation of the line parallel to the function 

We first start by finding the slope of the line in question, which we do by taking the derivative of 


We then use point slope form to get the equation of the line at the point
Example Question #10 : Derivatives
Find the equation of the line tangent to 







The first step is to find the derivative of the function given, which is 






Certified Tutor
Certified Tutor
All AP Calculus AB Resources