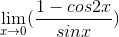All AP Calculus AB Resources
Example Questions
Example Question #13 : Calculus I — Derivatives
At the point 

The function is undefined at that point
Decreasing, convex
Increasing, concave
Decreasing, concave
Increasing, convex
Decreasing, convex
First, let's find out if the graph is increasing or decreasing. For that, we need the first derivative.
To find the first derivative, we can use the power rule. We lower the exponent on all the variables by one and multiply by the original variable.
We're going to treat 

Notice that 
Plug in our given point for 
Our result is negative, therefore the function is decreasing.
To find the concavity, look at the second derivative. If the function is positive at our given point, it is concave. If the function is negative, it is convex.
To find the second derivative we repeat the process, but using 
As you can see, our second derivative is a constant. It doesn't matter what point we plug in for 
Combine our two pieces of information to see that at the given point, the graph is decreasing and convex.
Example Question #1 : Finding Regions Of Concavity And Convexity
When 

There is insufficient data to solve.
Increasing, convex
Decreasing, convex
Increasing, concave
Decreasing, concave
Increasing, convex
To find the concavity, we need to look at the first and second derivatives at the given point.
To take the first derivative of this equation, use the power rule. The power rule says that we lower the exponent of each variable by one and multiply that number by the original exponent:
Simplify:
Remember that anything to the zero power is equal to one.
The first derivative tells us if the function is increasing or decreasing. Plug in the given point, 
Therefore the function is increasing.
To find out if the function is convex, we need to look at the second derivative evaluated at the same point, 
We're going to treat 

Notice that 
Plug in our given value:
Since the second derivative is positive, the function is convex.
Therefore, we are looking at a graph that is both increasing and convex at our given point.
Example Question #2 : Derivatives
At the point 

Increasing, concave
Decreasing, concave
The graph is undefined at point
Decreasing, convex
Increasing, convex
Decreasing, convex
To find out if the function is increasing or decreasing, we need to look at the first derivative.
To find the first derivative, we can use the power rule. We lower the exponent on all the variables by one and multiply by the original variable.
Anything to the zero power is one.
Now we plug in our given value and find out if the result is positive or negative. If it is positive, the function is increasing. If it is negative, the function is decreasing.
Therefore, the function is decreasing.
To find out if it is concave or convex, look at the second derivative. If the result is positive, it is convex. If it is negative, then it is concave.
To find the second derivative, we repeat the process using 
We're going to treat 

Notice that 
As stated before, anything to the zero power is one.
Since we get a positive constant, it doesn't matter where we look on the graph, as our second derivative will always be positive. That means that this graph is going to be convex at our given point.
Therefore, the function is decreasing and convex at our given point.
Example Question #2 : Derivatives
Define 
Give the interval(s) on which 

<0)
We need to find the values of 
&space;=&space;3x%5E%7B2%7D&space;-18x+24&space;<0)
These are the boundary points, so the intervals we need to check are:


We check each interval by substituting an arbitrary value from each for 
Choose

Choose

Choose

The answer is that 

Example Question #3 : Derivatives
Define &space;=&space;x%5E%7B3%7D&space;-&space;%5Cfrac%7B21%7D%7B2%7D&space;x%5E%7B2%7D&space;+30x&space;-6)
Give the interval(s) on which 

>0)
We need to find the values of 

These are the boundary points, so the intervals we need to check are:


We check each interval by substituting an arbitrary value from each for 
Choose

Choose

Choose

The answer is that 
Example Question #11 : Calculus I — Derivatives
At what point does 
It does not shift from increasing to decreasing
To find out where the graph shifts from increasing to decreasing, we need to look at the first derivative.
To find the first derivative, we can use the power rule. We lower the exponent on all the variables by one and multiply by the original variable.
We're going to treat 

Notice that 
If we were to graph 
Example Question #1 : Derivatives
At what value of 

It does not shift from decreasing to increasing
To find out when the function shifts from decreasing to increasing, we look at the first derivative.
To find the first derivative, we can use the power rule. We lower the exponent on all the variables by one and multiply by the original variable.
Anything to the zero power is one.
From here, we want to know if there is a point at which graph changes from negative to positive. Plug in zero for y and solve for x.
This is the point where the graph shifts from decreasing to increasing.
Example Question #2182 : High School Math
Evaluate the following limit:
When 



Example Question #1 : Derivative Interpreted As An Instantaneous Rate Of Change
Find the instantaneous rate of change for the function,
at the point 
Find the instantaneous rate of change for the function,
at the point 
1) First compute the derivative of the function, since this will give us the instantaneous rate of change of the function as a function of 
2) Now evaluate the derivative at the value 
Therefore, 


Example Question #1 : Derivative Interpreted As An Instantaneous Rate Of Change
A particle is traveling in a straight line along the x-axis with position function 

To find the instantaneous rate of change of the particle at time 



And

Hence the instantaneous rate of change in position (or just 'velocity') of the particle at 

Certified Tutor
All AP Calculus AB Resources




































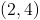


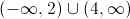

&space;=&space;3%5Ccdot&space;x%5E%7B3-1%7D&space;-2%5Ccdot&space;9x%5E%7B2-1%7D+24+0)