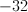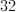To determine the equation of the line, we must first find its slope, which is parallel to that of the tangent line to the function. The tangent line to the function at any point is given by the first derivative of the function:

The following rule was used to find the derivative:

Evaluating the derivative at the given point, we find that the slope of the tangent line to the function is

We now can write the equation of the line using point-slope form:

To determine the equation of the line, we must first find its slope, which is perpendicular to that of the tangent line to the function. The tangent line to the function at any point is given by the first derivative of the function:

which was found using the following rules:

, 

Evaluating the derivative at the given point, we find that the slope of the tangent line to the function is

However, the line we want has a slope perpendicular to this, so we take the negative reciprocal:

We now can write the equation of the line using point-slope form:

Find the slope of the line tangent to the curve of f(x) when 

To find the slope of a tangent line, we need to find our first derivative.

To find our derivative, we need to recall two rules.

And

Using these two rules, we can find the derivative of f(x).

Our first term can be derived using our first rule. The derivative of e to the x is just e to the x.

This means that our first term will remain 16e to x.

For our other three terms, we follow the second rule. We will decrease each term's exponent by 1, and then multiply the coefficient by the old exponent.

Notice that the 13 will drop out. It is a constant term, and as such when we multiply it by it's original exponent (0) it wil be reduced to zero as well.

Clean up the above to get:

Now, we are almost there. We need to find the slope when x=-2. To do so, plug in -2 for x and solve.

So, our answer is -2350

To determine the equation of the line, we must first find its slope, which is perpendicular to that of the tangent line to the function. The tangent line to the function at any point is given by the first derivative of the function:

The first derivative was found using the following rules:

, , 

Evaluating the derivative at the given point, we get

Because the slope of the line we want is perpendicular to this line, its slope is the negative reciprocal, or

We can now find the equation of the line using point-slope form:

The slope of any point on this function can be determined by plugging the point's x-value into the , the first derivative of .

To find the tangent line at the given point, we need to first take the derivative of the given function. 

To find the derivative we need to use product rule. Product rule states that we take the derivative of the first function and multiply it by the derivative of the second function and then add that with the derivative of the second function multiplied by the given first function. To find the derivative of each separate function we need to use power rule. 

Power rule says that we take the exponent of the “x” value and bring it to the front. Then we subtract one from the exponent

Use power rule and we get : 

From here, to find the slope at the given point we plug in "2" for x.

This comes out to equal 

Since , by differentiating the position function twice, we see that acceleration is constant and . Acceleration, in this case, is gravity, which makes sense that it should be a constant value!

Notice that the function  is simply the derivative of  with respect to time. To see this, simply use the power rule on each of the two terms. 

Therefore,  is the rate at which the car's speed changes, a quantity called acceleration.

1) Recall the definition of a critical point: 

The critical points of a function  are defined as points , such that  is in the domain of , and at which the derivative  is either zero or does not exist. The number  is called a critical number of .  

2) Differentiate , 

3) Set to zero and solve for , 

The critical numbers are, 

We can also observe that the derivative does not exist at , since the term would be come infinite. However,  is not a critical number because the original function  is not defined at . The original function is infinite at , and therefore  is a vertical asymptote of  as can be seen in its' graph, 

Further Discussion

In this problem we were asked to obtain the critical numbers. If were were asked to find the critical points, we would simply evaluate the function at the critical numbers to find the corresponding function values and then write them as a set of ordered pairs, 

To answer this problem we must first interpret our given conditions: 

•  Implies the function is strictly increasing.
•  Implies the function is strictly concave down.

We note the only function given which fufills both of these conditions is .