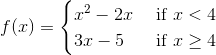1) If a function is differentiable, then by definition of differentiability the limit defined by, 

exists. Therefore (1) is required by definition of differentiability. _______________________________________________________________

2) If a function is differentiable at a point then it must also be continuous at that point. (This is not conversely true).

For a function to be continuous at a point  we must have: 

Therefore (2) and (4) are required. 

-----------------------------------------------------------------------------------------

3) 

This is not required, the left side of the equation is the definition of a derivative at a point  for a function . The derivative at a point does not have to equal to the function value  at that point, it is equal to the slope  at that point. Therefore 3 does not have to be true. 

However, we can note that it is possible for a function and its' derivative to be equal for a given point. Sine and cosine, for instance will intersect periodically. Another example would be the exponential function  which has itself as its' derivative . 

 ______________________________________________________________

 4) See 2

_______________________________________________________________ 

5) 

Again, the function does not have to approach the same limit as its' derivative. It is possible for a function to behave in this manner, such as in the case of sine and its' derivative cosine, which will both have the same limit at points where they intersect.  

By definition of differentiability,  when the limit exists. When  exists, we say the function is 'differentiable at '.

All of the functions are differentiable at . If you examine the graph of each of the functions, they are all defined at , and do not have a corner, cusp, or a jump there; they are all smooth and connected (Not necessarily everywhere, just at ). Additionally it is not possible to have a function that is differentiable at a point, but not continuous at that same point; differentiablity implies continuity.

To answer the question, we must find an equation which satisfies two criteria:

(1) it must have limits on either side of  that approach the same value and (2) it must have a hole at .

Each of the possible answers provide situations which demonstrate each combination of (1) and (2). That is to say, some of the equations include both a limit and a y-value at , neither, or,in the case of the piecewise function, a y-value and a limit that does not exist. 

In the function, , the numerator factors to  

while the denominator factors to . As a result, the graph of this

function resembles that for , but with a hole at . Therefore, the limit

at  exists, even though the y-value is undefined at .

To find the slope at a point, we take the derivative of , substitute in , and simplify.

.

.

First, use the chain rule to find f'(t).

You should get .

Next, plug in t=0 to get f'(0)=.

Find the derivative of the curve using the power rule.

In mathematical terms, the power rule states,

Therefore the derivative is,

Next, plug in the x-value to find the slope of the curve at , which gives you a final answer of 

Expand the binomial and combine like terms to get, 

Next, take the derivative of the polynomial using the power rule, which is in mathematical terms,

Therefore,

Lastly, plug in  for , to get the slope at the point.

This gives you your final answer of 

Derivatives are slope finders. Therefore to find the slope at the given point, we need to find the derivative of the function using power rule. Power rule says that we take the exponent of the “x” value and bring it to the front. Then we subtract one from the exponent.

So, we get 

From there we plug in our x value.

To find the slope at a point of our function, we need to find its derivative first.

Using the product rule (and the chain rule within this product rule application), we have

.

Plugging the -value of our point into this equation, we get our desired slope of

.