All AP Calculus AB Resources
Example Questions
Example Question #41 : Derivative As A Function
Find the intervals on which the function is decreasing:
To determine the intervals on which the function is decreasing, we must determine the intervals on which the function's first derivative is negative.
The first derivative of the function is equal to
and was found using the following rules:

Next, we must find the critical values, at which the first derivative is equal to zero:
Using the critical values, we now create intervals on which to evaluate the sign of the first derivative:
Notice how at the bounds of the intervals, the first derivative is neither positive nor negative.
Evaluating the sign simply by plugging in any value on the given interval into the first derivative function, we find that on the first interval, the first derivative is negative, and on the second interval, the first derivative is positive. We know, therefore, that the function is decreasing on the first interval, 
Example Question #42 : Derivative As A Function
Determine the relative minima of the function:
The function has no relative minima
To determine the values at which the function has a relative minimum, we must determine the intervals on which the function's first derivative changes from negative to positive.
The first derivative of the function is equal to
and was found using the following rules:

Next, we must find the critical values, at which the first derivative is equal to zero:
Using the critical values, we now create intervals on which to evaluate the sign of the first derivative:
Notice how at the bounds of the intervals, the first derivative is neither positive nor negative.
Evaluating the sign simply by plugging in any value on the given interval into the first derivative function, we find that on the first interval, the first derivative is positive, on the second interval, the first derivative is negative, and on the third interval, the first derivative is positive. Thus, the x value at which the function has a relative minimum is 
Example Question #43 : Derivative As A Function
For a function 





Given some arbitrary 


Positive or 0
Positive, Negative, or 0
Negative
Negative or 0
Positive
Positive or 0
Note that the derivative cannot be negative, because that would mean 






Carrying out the same analysis but with a positive derivative, we see that if 

Lastly, if the derivative is 0, then the function value didn't change. Thus, this would mean moving from 






Thus, as long as we're in 
Example Question #44 : Derivative As A Function
Explain whether f(x) is increasing or decreasing when 
f(x) is increasing when 
f(x) is increasing when 
f(x) is decreasing when 
f(x) is decreasing when 
f(x) is increasing when 
Explain whether f(x) is increasing or decreasing when 
To determine increasing or decreasing behavior, we need to know the sign of the first derivative at the given point. To do this, we will first find the first derivative, and then plug in our given point. This will tell us the slope of the tangent line to the original function at a particular point. Let's begin by finding our derivative.
To find our derivative, we need to recall two rules.
And
Using these two rules, we can find the derivative of f(x).
Our first term can be derived using our first rule. The derivative of e to the x is just e to the x.
This means that our first term will remain 16e to x.
For our other three terms, we follow the second rule. We will decrease each term's exponent by 1, and then multiply the coefficient by the old exponent.
Notice that the 13 will drop out. It is a constant term, and as such when we multiply it by it's original exponent (0) it wil be reduced to zero as well.
Clean up the above to get:
Now, we need to plug in 5 for x and see what our sign is.
Now, all that really matters for this question is the ultimate sign. Can you guess what it will be without calculating?
It is hugely positive! This makes sense, because we are raising two positive numbers to the fifth power. The only negative number we have comes from a linear term, so there is no way it will overcome the large positive terms.
So, our first derivative is positive at x=5. This means that f(x) is increasing when 
Example Question #45 : Derivative As A Function
Find the intervals on which the function is increasing:
To determine the intervals on which the function is increasing, we must determine the intervals on which the function's first derivative is positive.
The first derivative of the function is equal to
and was found using the following rules:


Next, we must find the critical values, at which the first derivative is equal to zero:
Note that the critical values are bounded by the interval in the problem statement.
Using the critical values, we now create intervals on which to evaluate the sign of the first derivative:
Notice how at the bounds of the intervals, the first derivative is neither positive nor negative.
Evaluating the sign simply by plugging in any value on the given interval into the first derivative function, we find that on the first interval, the first derivative is positive, on the second interval, the first derivative is negative, on the third interval, the first derivative is positive, and on the fourth interval, the first derivative is negative. So, the function is increasing on 
Example Question #46 : Derivative As A Function
Find the relative maxima of the following function:
The function has no relative maxima
The function has no relative maxima
To determine the values at which the function has a relative maximum, we must determine the intervals on which the function's first derivative changes from positive to negative.
The first derivative of the function is equal to
and was found using the following rules:


Next, we must find the critical values, at which the first derivative is equal to zero:
Using the critical values, we now create intervals on which to evaluate the sign of the first derivative:
Notice how at the bounds of the intervals, the first derivative is neither positive nor negative.
Evaluating the sign simply by plugging in any value on the given interval into the first derivative function, we find that on the first interval, the first derivative is positive, and on the second interval, the first derivative is positive. Because the first derivative never changed sign, the function has no relative extrema.
Example Question #47 : Derivative As A Function
Determine the intervals on which the function is decreasing:
The function is never decreasing
To determine the intervals on which the function is decreasing, we must determine the intervals on which the function's first derivative is negative.
The first derivative of the function is equal to
and was found using the following rules:


Next, we must find the critical values, at which the first derivative is equal to zero:
Using the critical values, we now create intervals on which to evaluate the sign of the first derivative:
Notice how at the bounds of the intervals, the first derivative is neither positive nor negative.
Evaluating the sign simply by plugging in any value on the given interval into the first derivative function, we find that on the first interval, the first derivative is negative, and on the second interval, the first derivative is negative as well. Thus, the function is decreasing on its entire domain, 
Example Question #48 : Derivative As A Function
Find the intervals on which the function is decreasing:
To determine the intervals on which the function is decreasing, we must determine the intervals on which the function's first derivative is negative.
The first derivative of the function is equal to
and was found using the following rules:

Next, we must find the critical values, at which the first derivative is equal to zero:
Using the critical values, we now create intervals on which to evaluate the sign of the first derivative:
Notice how at the bounds of the intervals, the first derivative is neither positive nor negative.
Evaluating the sign simply by plugging in any value on the given interval into the first derivative function, we find that on the first interval, the first derivative is negative, on the second interval, the first derivative is positive, on the third interval, the first derivative is negative, and on the fourth interval, the first derivative is positive. Thus, the function is decreasing on 
Example Question #41 : Relationship Between The Increasing And Decreasing Behavior Of ƒ And The Sign Of ƒ'
Find the intervals on which the function is increasing:
The function is never increasing
To determine the intervals on which the function is increasing, we must determine the intervals on which the function's first derivative is positive.
The first derivative of the function is equal to
and was found using the following rule:
Next, we must find the critical values, at which the first derivative is equal to zero:
Notice that the critical values are bounded by the interval given in the problem statement.
Using the critical values, we now create intervals on which to evaluate the sign of the first derivative:
Notice how at the bounds of the intervals, the first derivative is neither positive nor negative.
Evaluating the sign simply by plugging in any value on the given interval into the first derivative function, we find that on the first interval, the first derivative is negative, on the second interval, the first derivative is positive, and on the third interval, the first derivative is negative. Thus, the function is increasing on 
Example Question #42 : Derivative As A Function
Solve the separable differential equation:
To solve the separable differential equation, we must separate x and y to the same sides as their respective derivatives:
Next, we integrate both sides:
The integrals were solved using the following rule:
The two constants of integration were combined to make a single one.
Now, we use algebra to solve for y:
All AP Calculus AB Resources





























































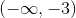
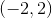
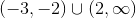


















![y=\sqrt[3]{\frac{3x^4}{4}+C}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1048699/gif.latex)

![y=\pm \sqrt[3]{\frac{3x^4}{4}+C}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1048700/gif.latex)
![y=\sqrt[3]{\frac{x^4}{4}+C}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1048702/gif.latex)



![y=\sqrt[3]{\frac{3x^4}{4}+C}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1048767/gif.latex)



