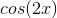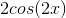Call Now to Set Up Tutoring:

(888) 888-0446

AP Calculus AB : Derivative as a function

Study concepts, example questions & explanations for AP Calculus AB

Create An Account

All AP Calculus AB Resources

3 Diagnostic Tests 164 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Mean Value Theorem

Find the mean value of the function f(x)=cos(x) over the interval $(0,\frac{\pi}{2})$ .

Possible Answers:

$c=cos^{-1}\frac{2}{\pi}$

$c=cos\frac{2}{\pi}$

$c=sin\frac{2}{\pi}$

$c=sin^{-1}\frac{2}{\pi}$

$c=sin^{-1}\frac{\pi}{2}$

Correct answer:

$c=sin^{-1}\frac{2}{\pi}$

Explanation:

To find the mean value of a function over some interval (a,b) , one mus use the formula: (f(b)-f(a))=(b-a)f'(c) .

Plugging in

$(f(\frac{\pi}{2})-f(0))=(\frac{\pi}{2})(-Sin(c))$

Simplifying

$-1=\frac{\pi}{2}(-Sin(c))$

$\frac{2}{\pi}=Sin(c)$

One must then use the inverse Sine function to find the value c:

$c=sin^{-1}\frac{2}{\pi}$

Report an Error

Example Question #1 : Equations Involving Derivatives

Practicing the chain rule level 1 B!

Find the derivative of the function

y(x)=(x+1)^2

Possible Answers:

2(x+1)

y'(x)=2x(x+1)^2

(x+1)

y'(x)=2x

y'(x)=x

Correct answer:

2(x+1)

Explanation:

To understand why the answer is

y'(x)=2(x+1) ,

you must understand that the derivative of

y(x)=x^2

is actually

y'(x)=2x .

Next, you must understand that the derivative of

y(x)=x+1

is actually

y'(x)=1 .

y(x)=(x+1)^2 can be treated as a composition of the functions

f(x)=x^2 and g(x)=x+1 .

in terms of f(x) and g(x) is actually f(g(x)) , which means

f(g(x))=(x+1)^2 since in x^2 is substituted with x+1 .

This means in order to differentiate the equation, you must use the chain rule. The chain rule tells us that in order to differentiate a composition function, you must differentiate all of the component composite functions in the reverse order that they are applied to the variable, one step at a time and multiply the results together.

the derivative of

y(x)=f(g(x))

Step 1: Only look at the outermost function f(x) first, then differentiate it

y(x)'=f'(...)

Step 2: Look at the next function g(x), keep it inside the other function f'(x).

y(x)'=f'(g(x))...

Step 3: Differentiate the the next function g(x) but multiply it by f'(g(x))

y(x)'=f'(g(x))*g'(x)

So, substitute f'(x), g(x) and g'(x) for the expressions you found before:

2*(x+1)*1

And now you have found the correct answer.

-------------------------------------------------------------------------------------------

To sum it up, you multiply the derivative of the outermost functions by the derivative if the inner function while keeping the next inner functions the the same in every step until you are out of functions to find the derivative of. This also applies to more complicated functions. For instance,

If we have

y=f(g(h(x)))

then it's derivative would be

y'=f'(g(h(x)))*g'(h(x))*h'(x)

Notice how the factors become less complicated as you differentiate it or as you look from left to right.

If you are unsure of the pattern, look at the pattern in these equations

Chain rule table

Report an Error

Example Question #2 : Equations Involving Derivatives

Practicing the chain rule level 1 A!

Find the derivative of the function

y=sin(2x)

Possible Answers:

cos(2x)

2sin(x)

2cos(2x)

2cos(x)

-2cos(2x)

Correct answer:

2cos(2x)

Explanation:

To understand why the answer is

y'=2cos(2x) ,

you must understand that the derivative of

y=sin(x)

is actually

y'=cos(x) .

Next, you must understand that the derivative of

y=2x

is actually

y'=2 .

y=sin(2x) can be treated as a composition of the functions

f(x)=sin(x) and g(x)=2x .

in terms of f(x) and g(x) is actually f(g(x)) , which means

f(g(x))=sin(2x) since in sin(x) is substituted with .

This means in order to differentiate the equation, you must use the chain rule. The chain rule tells us that in order to differentiate a composition function, you must differentiate all of the composite functions in the reverse order that they are applied to the variable, one step at a time and multiply the results together.

the derivative of

y=f(g(x))

Step 1: Only look at the outermost function f(x) first, then differentiate it

y'=f'(...)

Step 2: Look at the next function g(x), keep it inside the other function f'(x).

y'=f'(g(x))...

Step 3: Differentiate the the next function g(x) but multiply it by f'(g(x))

y'=f'(g(x))*g'(x)

So, substitute f'(x), g(x) and g'(x) for the expressions you found before:

cos(2x)*2

And now you have found the correct answer.

-------------------------------------------------------------------------------------------

If we have

y=f(g(h(x)))

then it's derivative would be

y'=f'(g(h(x)))*g'(h(x))*h'(x)

Notice how the factors become less complicated as you differentiate it or as you look from left to right.

If you are unsure of the pattern, look at the pattern in these equations

Chain rule table

Report an Error

Example Question #3 : Equations Involving Derivatives

Practicing the chain rule level 1 C!

Find the derivative of the function

$y(t)=e^{2x}$

Possible Answers:

$y'(x)=\frac{e^x}{2}$

$y'(t)=2e^{2x-1}$

$y'(t)=2x*e^{2x}$

$y'(t)=2*2^{2x-1}$

$y'(t)=2e^{2x}$

Correct answer:

$y'(t)=2e^{2x}$

Explanation:

To understand why the answer is

$y'(x)=2e^{2x}$ ,

you must understand that the derivative of

y(x)=e^x

is actually

y'(x)=e^x .

Next, you must understand that the derivative of

y(x)=2x

is actually

y'(x)=2 .

$y(x)=e^{2x}$ can be treated as a composition of the functions

f(x)=e^x and g(x)=2x .

in terms of f(x) and g(x) is actually f(g(x)) , which means

$f(g(x))=e^{2x}$ since in e^x is substituted with .

the derivative of

y(x)=f(g(x))

Step 1: Only look at the outermost function f(x) first, then differentiate it

y'(x)=f'(...)

Step 2: Look at the next function g(x), keep it inside the other function f'(x).

y'(x)=f'(g(x))...

Step 3: Differentiate the the next function g(x) but multiply it by f'(g(x))

y'(x)=f'(g(x))*g'(x)

So, substitute f'(x), g(x) and g'(x) for the expressions you found before:

$y'(x)=2e^{2x}$

And now you have found the correct answer.

-------------------------------------------------------------------------------------------

If we have

y=f(g(h(x)))

then it's derivative would be

y'=f'(g(h(x)))*g'(h(x))*h'(x)

Notice how the factors become less complicated as you differentiate it or as you look from left to right.

If you are unsure of the pattern, look at the pattern in these equations

Chain rule table

Report an Error

Example Question #3 : Equations Involving Derivatives

Practicing the chain rule level 1 D!

Find the derivative of the function

$p(x)=\frac{2}{2-3x}$

Possible Answers:

$p'(x)=\frac{9x^2+6}{(2-3x)^2}$

$p'(x)=\frac{-2}{3x(2-3x)}$

$p'(x)=\frac{6}{(2-3x)^2}$

$p'(x)=\frac{-3x}{4-3x^2}$

p'(x)=-6x

Correct answer:

$p'(x)=\frac{6}{(2-3x)^2}$

Explanation:

To understand why the answer is

$p'(x)=\frac{6}{(2-3x)^2}$ ,

you must understand that the derivative of

$y(x)=\frac{1}{x}$

is actually

$y(x)'=\frac{-1}{x^2}$ .

Next, you must understand that the derivative of

y(x)=2-3x

is actually

y(x)'=-3 .

$p(x)=\frac{2}{-3x+2}$ can be treated as a composition of the functions

$f(x)=\frac{1}{x}$ and g(x)=2-3x .

p(x) in terms of f(x) and g(x) is actually f(g(x)) and

$f(g(x))=\frac{2}{-3x+2}$ since in $\frac{1}{x}$ is substituted with 2-3x .

the derivative of

p(x)=f(g(x))

is...

Step 1: Only look at the outermost function f(x) first, then differentiate it

p(x)'=f'(...)

Step 2: Look at the next function g(x), keep it inside the other function f'(x).

p(x)'=f'(g(x))...

Step 3: Differentiate the the function g(x) but multiply its derivative by f'(g(x))

p(x)'=f'(g(x))*g'(x)

So, substitute f'(x), g(x) and g'(x) for the expressions you found before:

$p'(x)=\frac{6}{(2-3x)^2}$

And now you have found the correct answer.

-------------------------------------------------------------------------------------------

To sum it up, you multiply the derivative of the outermost functions by the derivative if the inner function while keeping the next inner functions the same in every step until you are out of functions to find the derivative of. This also applies to more complicated functions. For instance,

If we have

y=f(g(h(x)))

then it's derivative would be

y'=f'(g(h(x)))*g'(h(x))*h'(x)

Notice how the factors become less complicated as you differentiate it or as you look from left to right.

If you are unsure of the pattern, look at the pattern in these equations

Chain rule table

Report an Error

Example Question #65 : Derivative As A Function

Practicing the chain rule level 2 A!

Find the derivative of the function

$p(x)=e^{^{x^{3}}}$

Possible Answers:

$p'(x)=(3x^{^{2}}-1)*e^{^{x^3}-1}$

$p'(x)=x^{^{2}}*e^{^{x^{^{3}}-1}}$

$p'(x)=e^{x^{3}}$

$p'(x)=3e^{x^{2}}$

$p'(x)=3x^{2}*e^{x^{3}}$

Correct answer:

$p'(x)=3x^{2}*e^{x^{3}}$

Explanation:

To understand why the answer is

$p'(x)=3x^{2}*e^{x^3}$ ,

you must understand that the derivative of

y(x)=e^x

is actually

y'(x)=e^x .

Next, you must understand that the derivative of

y(x)=x^3

is actually

y'(x)=3x^2 .

$p(x)=e^{x^{3}}$ can be treated as a composition of the functions

f(x)=e^x and $g(x)=x^{3}$ .

p(x) in terms of f(x) and g(x) is actually f(g(x)) and

$f(g(x))=e^{x^{3}}$ since in e^x is substituted with $x^{3}$ .

This means in order to differentiate the equation, you must use the chain rule. The chain rule tells us that in order to differentiate a composition function, you must differentiate all of the composite functions in the reverse order that they are applied to the variable one step at a time and multiply the results together.

the derivative of

p(x)=f(g(x))

is...

Step 1: Only look at the outermost function f(x) first, then differentiate it

p'(x)=f'(...)

Step 2: Look at the next function g(x), keep it inside the other function f'(x).

p'(x)=f'(g(x))...

Step 3: Differentiate the the function g(x) but multiply its derivative by f'(g(x))

p'(x)=f'(g(x))*g'(x)

So, substitute f'(x), g(x) and g'(x) for the expressions you found before:

$p'(x)=3x^{2}*e^{x^{3}}$

And now you have found the correct answer.

-------------------------------------------------------------------------------------------

If we have

y=f(g(h(x)))

then it's derivative would be

y'=f'(g(h(x)))*g'(h(x))*h'(x)

Notice how the factors become less complicated as you differentiate it or as you look from left to right.

If you are unsure of the pattern, look at the pattern in these equations

Chain rule table

Report an Error

Example Question #4 : Equations Involving Derivatives

Practicing the chain rule level 2 B!

Find the derivative of the function

$p(t)=tan^{2}(t)$

Possible Answers:

$p'(t)=\frac{sin(t)}{2cos^2(t)}$

p'(t)=2tan(t)

p'(t)=2sec^2(t)

p'(t)=2tan(t)*sec^2(t)

p'(t)=-2cot(t)*csc(t)

Correct answer:

p'(t)=2tan(t)*sec^2(t)

Explanation:

To understand why the answer is

p'(t)=2tan(t)sec(t) ,

you must understand that the derivative of

p(t)=t^2

is actually

p'(t)=2t .

Next, you must understand that the derivative of

p(t)=tan(t)

is actually

p'(t)=sec^2(t) .

p(t)=tan^2(t) can be treated as a composition of the functions

f(t)=t^2 and g(t)=tan(t) .

p(t) in terms of f(t) and g(t) is actually f(g(t)) which means

f(g(t))=tan^2(t) since in t^2 is substituted with tan(t) .

This means in order to differentiate the equation, you must use the chain rule. The chain rule tells us that in order to differentiate a composition function, you must differentiate all of the composite functions in the reverse order that they are applied to the variable one step at a time and multiply the results together.

the derivative of

p(t)=f(g(t))

is...

Step 1: Only look at the outermost function f(x) first, then differentiate it

p'(t)=f'(...)

Step 2: Look at the next function g(x), keep it inside the other function f'(x).

p'(t)=f'(g(t))...

Step 3: Differentiate the the next function g(x) but multiply it by f'(g(x))

p'(t)=f'(g(t))*g'(t)

So, substitute f'(t), g(t) and g'(t) for the expressions you found before:

y'(t)=2tan(t)sec^2(t)

And now you have found the correct answer.

-------------------------------------------------------------------------------------------

If we have

y=f(g(h(x)))

then it's derivative would be

y'=f'(g(h(x)))*g'(h(x))*h'(x)

Notice how the factors become less complicated as you differentiate it or as you look from left to right.

If you are unsure of the pattern, look at the pattern in these equations

Chain rule table

Report an Error

Example Question #5 : Equations Involving Derivatives

Practicing the chain rule level 2 C!

Find the derivative of the function

$y(x)=\frac{-1}{2^{x}-4}$

Possible Answers:

$y'(x)=\frac{-ln(2)}{2^x-4}$

$y'(x)=\frac{-1}{ln(2)(2^x-4)^2}$

$y'(x)=\frac{2^x*ln(2)}{(2^x-4)^2}$

$y'(x)=\frac{-ln(2)(2^x-4)}{(2^x-4)^2}$

$y'(x)=\frac{2x}{2^x-4}$

Correct answer:

$y'(x)=\frac{2^x*ln(2)}{(2^x-4)^2}$

Explanation:

To understand why the answer is

$y'(x)=\frac{2^x*ln(2)}{(2^x-4)^2}$

you must understand that the derivative of

$y(x)=\frac{-1}{x}$

is actually

$y'(x)=\frac{1}{x^2}$ .

Next, you must understand that the derivative of

y(x)=2^x-4

is actually

y'(x)=2^x*ln(2) .

$y(x)=\frac{-1}{2^x-4}$ can be treated as a composition of the functions

$f(x)=\frac{1}{x}$ and g(x)=2^x-4 .

y(x) in terms of f(x) and g(x) is actually f(g(x)) which means

$f(g(x))=\frac{-1}{2^x-4}$ since in $\frac{-1}{x}$ is substituted with 2^x-4 .

This means in order to differentiate the equation, you must use the chain rule. The chain rule tells us that in order to differentiate a composition function, you must differentiate all of the composite functions in the reverse order that they are applied to the variable, one step at a time and multiply the results together.

the derivative of

y(x)=f(g(x))

is...

Step 1: Only look at the outermost function f(x) first, then differentiate it

y(x)'=f'(...)

Step 2: Look at the next function g(x), keep it inside the other function f'(x).

y(x)'=f'(g(x))...

Step 3: Differentiate the the next function g(x) but multiply it by f'(g(x))

y(x)'=f'(g(x))*g'(x)

So, substitute f'(x), g(x) and g'(x) for the expressions you found before:

$y'(x)=\frac{2^x*ln(2)}{(2^x-4)^2}$

And now you have found the correct answer.

-------------------------------------------------------------------------------------------

If we have

y=f(g(h(x)))

then it's derivative would be

y'=f'(g(h(x)))*g'(h(x))*h'(x)

Notice how the factors become less complicated as you differentiate it or as you look from left to right.

If you are unsure of the pattern, look at the pattern in these equations

Chain rule table

Report an Error

Example Question #6 : Equations Involving Derivatives

Practicing the chain rule level 2 D!

Find the derivative of the function

y(x)=ln(arccos(x))

Possible Answers:

$y'(x)=\frac{-1}{arccos(x)}$

$y'(x)=\frac{-1}{\sqrt{1-x^2}*arccos(x)}$

$y'(x)=\sqrt{1-x^2}$

$y'(x)=\frac{ln(arccos(x))}{\sqrt{1-x^2}}$

$y'(x)=\frac{\sqrt{1-x^2}}{arccos(x)}$

Correct answer:

$y'(x)=\frac{-1}{\sqrt{1-x^2}*arccos(x)}$

Explanation:

To understand why the answer is

$y'(x)=\frac{-1}{\sqrt{1-x^2}*arccos(x)}$ ,

you must understand that the derivative of

y(x)=ln(x)

is actually

$y'(x)=\frac{1}{x}$ .

Next, you must understand that the derivative of

y(x)=arccos(x)

is actually

$y'(x)=\frac{-1}{\sqrt{1-x^2}}$ .

y(x)=ln(arccos(x)) can be treated as a composition of the functions

$f(x)=\frac{1}{x}$ and g(x)=arccos(x) .

y(x) in terms of f(x) and g(x) is actually f(g(x)) which means

f(g(x))=ln(arccos(x)) since in ln(x) is substituted with .

This means in order to differentiate the equation, you must use the chain rule. The chain rule tells us that in order to differentiate a composition function, you must differentiate all of the composite functions in the reverse order that they are applied to the variable, one step at a time and multiply the results together.

the derivative of

y(x)=f(g(x))

is...

Step 1: Only look at the outermost function f(x) first, then differentiate it

y(x)'=f'(...)

Step 2: Look at the next function g(x), keep it inside the other function f'(x).

y(x)'=f'(g(x))...

Step 3: Differentiate the the next function g(x) but multiply it by f'(g(x))

y(x)'=f'(g(x))*g'(x)

So, substitute f'(x), g(x) and g'(x) for the expressions you found before:

$y'(x)=\frac{-1}{\sqrt{1-x^2}*arccos(x)}$

And now you have found the correct answer.

-------------------------------------------------------------------------------------------

If we have

y=f(g(h(x)))

then it's derivative would be

y'=f'(g(h(x)))*g'(h(x))*h'(x)

Notice how the factors become less complicated as you differentiate it or as you look from left to right.

If you are unsure of the pattern, look at the pattern in these equations

Chain rule table

Report an Error

Example Question #7 : Equations Involving Derivatives

Practicing the chain rule level 3 A!

Find the derivative of the function

$y(x)=ln(\sqrt{sin(x^2)})$

Possible Answers:

y'(x)=2x*sin(x^2)*cos(x)

y'(x)=x*cot(x^2)

y'(x)=tan(x^2)

$y'(x)=\frac{1}{2}ln(sin(x^{2}))*cos(x^2)$

$y'(x)=\frac{x}{cos(x^2)}$

Correct answer:

y'(x)=x*cot(x^2)

Explanation:

To understand why the answer is

y(x)'=x*cot(x^2) ,

first remember that ln(x^a)=a*ln(x) .

Then, you must understand that the derivative of

y(x)=ln(x)

is actually

y'(x)=1/x .

Next, you must understand that the derivative of

y(x)=sin(x)

is actually

y'(x)=cos(x) .

And finally, you must understand that the derivative of

y(x)=x^2

is actually

y'(x)=2x .

$y(x)=ln(\sqrt{sin(x^2)})$ can be treated as a composition of the functions

f(x)=ln(x) , $g(x)=\sqrt{sin(x)}$ and h(x)=x^2 .

The reason why we did not define $g(x)=\sqrt{x}$ , h(x)=sin(x) and m(x)=x^2

is because of the property ln(x^a)=a*ln(x) mentioned before,

turning

$ln(\sqrt{g(h(x))})$

into

$\frac{1}{2}*ln(g(h(x)))$

y(x) in terms of f(x) , g(x) and h(x) is actually f(g(h(x))) which means

$f(g(h(x)))=\frac{1}{2}*ln(sin(x^2))$ since in ln(x) is substituted with sin(x) and in sin(x) can be substituted with x^2 .

This means in order to differentiate the equation, you must use the chain rule. The chain rule tells us that in order to differentiate a composition function, you must differentiate all of the composite functions in the reverse order that they are applied to the variable one step at a time and multiply the results together.

the derivative of

y(x)=f(g(h(x)))

is...

Step 1: Only look at the outermost function f(x) first, then differentiate it

y'(x)=f'(...)

Step 2: Look at the next function g(x), keep it inside the other function f'(x).

y'(x)=f'(g(...))...

Step 3: Look at the next function h(x), keep it inside the other function g(x)

y'(x)=f'(g(h(x)))

Step 4: Differentiate the the next function g(x) while keeping h(x) inside of g(x) and g'(x). But, multiply g'(h(x)) by f'(g(h(x)))

y'(x)=f'(g(h(x)))*g'(h(x))...

Step 5: Differentiate the next function h(x) but multiply it by the factors f'(g(h(x)))*g'(h(x))

f'(g(h(x)))*g'(h(x))*h'(x)

Since you are out of composite functions to differentiate, stop here.

Now, substitute f'(x), g(x), g'(x), h(x) and h'(x) for the expressions you found before:

$\frac{1}{2}\frac{1}{sin(x^2)}*cos(x^2)*2x$ which is x*cot(x^2)

and now you have found the correct answer.

-------------------------------------------------------------------------------------------

To sum it up, you multiply the derivative of the outermost functions by the derivative if the inner functions while keeping the next inner functions the same in every step until you are out of functions to find the derivative of. This also applies to more complicated functions. For instance,

If we have

y=f(g(h(m(x))))

then it's derivative would be

y'=f'(g(h(m(x))))*g'(h(m(x)))*h'(m(x))*m'(x)

Notice how the factors become less complicated as you differentiate it or as you look from left to right.

If you are unsure of the pattern, look at the pattern in the table below.

Chain rule table

Report an Error

View AP Calculus AB Tutors

Sharif
Certified Tutor

NCCU, Bachelors, Physics and Mathematics.

View AP Calculus AB Tutors

Muhammad
Certified Tutor

The University of Texas at Dallas, Bachelor of Science, Mechanical Engineering.

View AP Calculus AB Tutors

Megan
Certified Tutor

University of Wisconsin-Madison, Bachelor of Science, Chemical Engineering.

All AP Calculus AB Resources

3 Diagnostic Tests 164 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Math Tutors in Los Angeles, French Tutors in Los Angeles, GRE Tutors in New York City, MCAT Tutors in San Francisco-Bay Area, Calculus Tutors in Los Angeles, Reading Tutors in Boston, Algebra Tutors in Atlanta, Physics Tutors in San Diego, Biology Tutors in Atlanta, Biology Tutors in Phoenix

Popular Courses & Classes

SSAT Courses & Classes in Phoenix, GRE Courses & Classes in Seattle, LSAT Courses & Classes in San Diego, GMAT Courses & Classes in Washington DC, Spanish Courses & Classes in Chicago, Spanish Courses & Classes in Phoenix, ISEE Courses & Classes in Dallas Fort Worth, GMAT Courses & Classes in San Francisco-Bay Area, GRE Courses & Classes in San Diego, ISEE Courses & Classes in Seattle

Popular Test Prep

ISEE Test Prep in Boston, SSAT Test Prep in Los Angeles, ACT Test Prep in Dallas Fort Worth, SAT Test Prep in Miami, GRE Test Prep in Seattle, SSAT Test Prep in Phoenix, ISEE Test Prep in San Francisco-Bay Area, SSAT Test Prep in San Francisco-Bay Area, SSAT Test Prep in San Diego, GMAT Test Prep in Seattle

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

AP Calculus AB : Derivative as a function

Study concepts, example questions & explanations for AP Calculus AB

All AP Calculus AB Resources

Example Questions

Example Question #1 : Mean Value Theorem

Example Question #1 : Equations Involving Derivatives

Example Question #2 : Equations Involving Derivatives

Example Question #3 : Equations Involving Derivatives

Example Question #3 : Equations Involving Derivatives

Example Question #65 : Derivative As A Function

Example Question #4 : Equations Involving Derivatives

Example Question #5 : Equations Involving Derivatives

Example Question #6 : Equations Involving Derivatives

Example Question #7 : Equations Involving Derivatives

All AP Calculus AB Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: