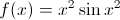We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

AP Calculus AB : AP Calculus AB

Study concepts, example questions & explanations for AP Calculus AB

Create An Account

All AP Calculus AB Resources

3 Diagnostic Tests 164 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #45 : Interpretations And Properties Of Definite Integrals

$\begin{align*}&\int_{-3}^{3}f(x)dx=95\\&\int_{15}^{3}f(x)dx=-81\\&\int_{-3}^{26}f(x)dx=154\\&\text{Use the above values to find }\int_{26}^{15}f(x)dx\end{align*}$

Possible Answers:

140

Correct answer:

Explanation:

$\begin{align*}&\text{A principle of integrals is one of summation. If the values}\\&\text{of an integral across given sets of points is known, they could}\\&\text{ be used to find integral values across other points. Imagine}\\&\text{a set of points that are in ascending numerical value: a, b,}\\&\text{c, and d. It follows that:}\\&\int_a^d=\int_a^b+\int_b^c+\int_c^d\text{ and likewise: }\int_a^d-\int_a^b-\int_b^c=\int_c^d\\&\text{Also, if an integral value is known, the same integral backwards}\\&\text{will give a negative of the original value:}\\&\int_a^b=-\int_b^a\\&\text{Knowing all this, we can calculate }\int_{26}^{15}f(x)dx\\&\int_{-3}^{26}f(x)dx=\int_{-3}^{3}f(x)dx-\int_{15}^{3}f(x)dx-\int_{26}^{15}f(x)dx\\&-\int_{26}^{15}f(x)dx=\int_{-3}^{26}f(x)dx-\int_{-3}^{3}f(x)dx+\int_{15}^{3}f(x)dx\\&-\int_{26}^{15}f(x)dx=154-(95)+(-81)\\&\int_{26}^{15}f(x)dx=22\\&\end{align*}$

Report an Error

Example Question #21 : Basic Properties Of Definite Integrals (Additivity And Linearity)

$\begin{align*}&\int_{-4}^{-3}f(x)dx=66\\&\int_{-3}^{4}f(x)dx=-32\\&\int_{6}^{14}f(x)dx=25\\&\int_{-4}^{14}f(x)dx=3\\&\text{Calculate from the above values }\int_{6}^{4}f(x)dx\end{align*}$

Possible Answers:

Correct answer:

Explanation:

$\begin{align*}&\text{A principle of integrals is one of summation. If the values}\\&\text{of an integral across given sets of points is known, they could}\\&\text{ be used to find integral values across other points. Imagine}\\&\text{a set of points that are in ascending numerical value: a, b,}\\&\text{c, and d. It follows that:}\\&\int_a^d=\int_a^b+\int_b^c+\int_c^d\text{ and likewise: }\int_a^d-\int_a^b-\int_b^c=\int_c^d\\&\text{Also, if an integral value is known, the same integral backwards}\\&\text{will give a negative of the original value:}\\&\int_a^b=-\int_b^a\\&\text{Knowing all this, we can calculate }\int_{6}^{4}f(x)dx\\&\int_{-4}^{14}f(x)dx=\int_{-4}^{-3}f(x)dx+\int_{-3}^{4}f(x)dx-\int_{6}^{4}f(x)dx+\int_{6}^{14}f(x)dx\\&-\int_{6}^{4}f(x)dx=\int_{-4}^{14}f(x)dx-\int_{-4}^{-3}f(x)dx-\int_{-3}^{4}f(x)dx-\int_{6}^{14}f(x)dx\\&-\int_{6}^{4}f(x)dx=3-(66)-(-32)-(25)\\&\int_{6}^{4}f(x)dx=56\\&\end{align*}$

Report an Error

Example Question #22 : Basic Properties Of Definite Integrals (Additivity And Linearity)

$\begin{align*}&\int_{10}^{19}f(x)dx=-40\\&\int_{19}^{30}f(x)dx=1\\&\int_{42}^{30}f(x)dx=-12\\&\int_{4}^{42}f(x)dx=-19\\&\text{Use the above values to find }\int_{10}^{4}f(x)dx\end{align*}$

Possible Answers:

Correct answer:

Explanation:

$\begin{align*}&\text{A principle of integrals is one of summation. If the values}\\&\text{of an integral across given sets of points is known, they could}\\&\text{ be used to find integral values across other points. Imagine}\\&\text{a set of points that are in ascending numerical value: a, b,}\\&\text{c, and d. It follows that:}\\&\int_a^d=\int_a^b+\int_b^c+\int_c^d\text{ and likewise: }\int_a^d-\int_a^b-\int_b^c=\int_c^d\\&\text{Also, if an integral value is known, the same integral backwards}\\&\text{will give a negative of the original value:}\\&\int_a^b=-\int_b^a\\&\text{Knowing all this, we can calculate }\int_{10}^{4}f(x)dx\\&\int_{4}^{42}f(x)dx=-\int_{10}^{4}f(x)dx+\int_{10}^{19}f(x)dx+\int_{19}^{30}f(x)dx-\int_{42}^{30}f(x)dx\\&-\int_{10}^{4}f(x)dx=\int_{4}^{42}f(x)dx-\int_{10}^{19}f(x)dx-\int_{19}^{30}f(x)dx+\int_{42}^{30}f(x)dx\\&-\int_{10}^{4}f(x)dx=-19-(-40)-(1)+(-12)\\&\int_{10}^{4}f(x)dx=-8\\&\end{align*}$

Report an Error

Example Question #23 : Basic Properties Of Definite Integrals (Additivity And Linearity)

$\begin{align*}&\int_{-4}^{1}f(x)dx=-81\\&\int_{14}^{10}f(x)dx=80\\&\int_{14}^{24}f(x)dx=-4\\&\int_{24}^{31}f(x)dx=96\\&\int_{-4}^{31}f(x)dx=-11\\&\text{Use the above values to find }\int_{10}^{1}f(x)dx\end{align*}$

Possible Answers:

102

Correct answer:

Explanation:

$\begin{align*}&\text{A principle of integrals is one of summation. If the values}\\&\text{of an integral across given sets of points is known, they could}\\&\text{ be used to find integral values across other points. Imagine}\\&\text{a set of points that are in ascending numerical value: a, b,}\\&\text{c, and d. It follows that:}\\&\int_a^d=\int_a^b+\int_b^c+\int_c^d\text{ and likewise: }\int_a^d-\int_a^b-\int_b^c=\int_c^d\\&\text{Also, if an integral value is known, the same integral backwards}\\&\text{will give a negative of the original value:}\\&\int_a^b=-\int_b^a\\&\text{Knowing all this, we can calculate }\int_{10}^{1}f(x)dx\\&\int_{-4}^{31}f(x)dx=\int_{-4}^{1}f(x)dx-\int_{10}^{1}f(x)dx-\int_{14}^{10}f(x)dx+\int_{14}^{24}f(x)dx+\int_{24}^{31}f(x)dx\\&-\int_{10}^{1}f(x)dx=\int_{-4}^{31}f(x)dx-\int_{-4}^{1}f(x)dx+\int_{14}^{10}f(x)dx-\int_{14}^{24}f(x)dx-\int_{24}^{31}f(x)dx\\&-\int_{10}^{1}f(x)dx=-11-(-81)+(80)-(-4)-(96)\\&\int_{10}^{1}f(x)dx=-58\\&\end{align*}$

Report an Error

Example Question #24 : Basic Properties Of Definite Integrals (Additivity And Linearity)

$\begin{align*}&\int_{0}^{4}f(x)dx=67\\&\int_{5}^{4}f(x)dx=-6\\&\int_{8}^{22}f(x)dx=72\\&\int_{22}^{23}f(x)dx=-54\\&\int_{0}^{23}f(x)dx=96\\&\text{Calculate from the above values }\int_{8}^{5}f(x)dx\end{align*}$

Possible Answers:

Correct answer:

Explanation:

$\begin{align*}&\text{A principle of integrals is one of summation. If the values}\\&\text{of an integral across given sets of points is known, they could}\\&\text{ be used to find integral values across other points. Imagine}\\&\text{a set of points that are in ascending numerical value: a, b,}\\&\text{c, and d. It follows that:}\\&\int_a^d=\int_a^b+\int_b^c+\int_c^d\text{ and likewise: }\int_a^d-\int_a^b-\int_b^c=\int_c^d\\&\text{Also, if an integral value is known, the same integral backwards}\\&\text{will give a negative of the original value:}\\&\int_a^b=-\int_b^a\\&\text{Knowing all this, we can calculate }\int_{8}^{5}f(x)dx\\&\int_{0}^{23}f(x)dx=\int_{0}^{4}f(x)dx-\int_{5}^{4}f(x)dx-\int_{8}^{5}f(x)dx+\int_{8}^{22}f(x)dx+\int_{22}^{23}f(x)dx\\&-\int_{8}^{5}f(x)dx=\int_{0}^{23}f(x)dx-\int_{0}^{4}f(x)dx+\int_{5}^{4}f(x)dx-\int_{8}^{22}f(x)dx-\int_{22}^{23}f(x)dx\\&-\int_{8}^{5}f(x)dx=96-(67)+(-6)-(72)-(-54)\\&\int_{8}^{5}f(x)dx=-5\\&\end{align*}$

Report an Error

Example Question #21 : Basic Properties Of Definite Integrals (Additivity And Linearity)

$\begin{align*}&\int_{1}^{7}f(x)dx=16\\&\int_{13}^{28}f(x)dx=-82\\&\int_{1}^{28}f(x)dx=-30\\&\text{Use the above values to find }\int_{13}^{7}f(x)dx\end{align*}$

Possible Answers:

Correct answer:

Explanation:

$\begin{align*}&\text{A principle of integrals is one of summation. If the values}\\&\text{of an integral across given sets of points is known, they could}\\&\text{ be used to find integral values across other points. Imagine}\\&\text{a set of points that are in ascending numerical value: a, b,}\\&\text{c, and d. It follows that:}\\&\int_a^d=\int_a^b+\int_b^c+\int_c^d\text{ and likewise: }\int_a^d-\int_a^b-\int_b^c=\int_c^d\\&\text{Also, if an integral value is known, the same integral backwards}\\&\text{will give a negative of the original value:}\\&\int_a^b=-\int_b^a\\&\text{Knowing all this, we can calculate }\int_{13}^{7}f(x)dx\\&\int_{1}^{28}f(x)dx=\int_{1}^{7}f(x)dx-\int_{13}^{7}f(x)dx+\int_{13}^{28}f(x)dx\\&-\int_{13}^{7}f(x)dx=\int_{1}^{28}f(x)dx-\int_{1}^{7}f(x)dx-\int_{13}^{28}f(x)dx\\&-\int_{13}^{7}f(x)dx=-30-(16)-(-82)\\&\int_{13}^{7}f(x)dx=-36\\&\end{align*}$

Report an Error

Example Question #51 : Interpretations And Properties Of Definite Integrals

Given that $\int_{5}^{1}(2u)dx = 8$ and $\int_{3}^{2}(-u)dx = 4$ , find the value of the following expression:

$\int_{1}^{3}(u)dx - \int_{5}^{4}(u)dx + \int_{2}^{4}(u)dx$

Possible Answers:

Correct answer:

Explanation:

First, simplifying the given's gives us

$\int_{5}^{1}(2u)dx = -2\int_{1}^{5}(u)dx = 8$

$\int_{1}^{5}(u)dx = -4$

And

$\int_{3}^{2}(-u)dx = \int_{2}^{3}(u)dx = 4$

Our goal is to get the given expression into terms of these two integrals. Our first step will be to try and get a $\int_{1}^{5}(u)dx$ from our expression.

First note,

$-\int_{5}^{4}(u)dx = \int_{4}^{5}(u)dx$

And for the third term,

$\int_{2}^{4}(u)dx = \int_{2}^{3}(u)dx + \int_{3}^{4}(u)dx$

Putting these facts together, we can rewrite the original expression as

$\int_{1}^{3}(u)dx +(\int_{4}^{5}(u)dx) + (\int_{2}^{3}(u)dx + \int_{3}^{4}(u)dx)$

Rearranging,

$(\int_{1}^{3}(u)dx + \int_{3}^{4}(u)dx + \int_{4}^{5}(u)dx) + \int_{2}^{3}(u)dx$

The three terms in parentheses can all be brought together, as the top limit of the previous integral matches the bottom limit of the next integral. Thus, we now have

$\int_{1}^{5}(u)dx + \int_{2}^{3}(u)dx$

Substituting in our given's, this simplifies to -4 + 4 = 0

Report an Error

Example Question #21 : Basic Properties Of Definite Integrals (Additivity And Linearity)

Evaluate the definite integral

$\int_{\pi}^{0}4(3x^2-sin(x)+2)dx$

Possible Answers:

$12\pi^2$

$-12\pi^2$

$4\pi^3+8\pi-8$

$-4\pi^3-8\pi+8$

Correct answer:

$-4\pi^3-8\pi+8$

Explanation:

Here we are using several basic properties of definite integrals as well as the fundamental theorem of calculus.

First, you can pull coefficients out to the front of integrals.

$\int_{\pi}^{0}4(3x^2-sin(x)+2)dx=4\int_{\pi}^{0}(3x^2-sin(x)+2)dx$

Second, we notice that our lower bound is bigger than our upper bound. You can switch the upper and lower bounds if you also switch the sign.

$4\int_{\pi}^{0}(3x^2-sin(x)+2)dx=-4\int_{0}^{\pi}(3x^2-sin(x)+2)dx$

Lastly, our integral "distributes" over addition and subtraction. That means you can split the integral by each term and integrate each term separately.

$-4\int_{0}^{\pi}(3x^2-sin(x)+2)dx=-4(\int_{0}^{\pi}3x^2dx-\int_{0}^{\pi}sin(x)dx+\int_{0}^{\pi}2dx)$

Now we integrate and calculate using the Fundamental Theorem of Calculus.

$-4(x^3+cos(x)+2x)]_{0}^{\pi}=-4[(\pi^3+cos(\pi)+2\pi)-(0^3+cos(0)+2(0))]$

$=-4[(\pi^3-1+2\pi)-1]=-4\pi^3-8\pi+8$

Report an Error

Example Question #52 : Interpretations And Properties Of Definite Integrals

Solve:

$\int_{0}^{2} x dx+\int_{0}^{2}x^2dx$

Possible Answers:

$\frac{2}{3}$

None of the other answers

$\frac{14}{3}$

$\frac{8}{3}$

Correct answer:

$\frac{14}{3}$

Explanation:

Rather than solve each integral independently, we can use the property of linearity to add the integrals together:

$\int_{0}^{2} x dx+\int_{0}^{2}x^2dx = \int_{0}^{2}(x+x^2)dx=\frac{x^2}{2}+\frac{x^3}{3}\left.\begin{matrix} 2\\0 \end{matrix}\right|$

The integrals were solved using the following rule:

$\int x^n dx=\frac{x^{n+1}}{n+1}+C$

Finally, we evaluate the definite integral by evaluating the answer at the upper bound and subtracting the answer evaluated at the lower bound:

$\frac{8}{3}+2-(0+0)=\frac{14}{3}$

Report an Error

Example Question #1 : Continunity As A Property Of Functions

Which of the following functions contains a removeable discontinuity?

Possible Answers:

$f(x)=\frac{x}{1-x^{2}}$

$f(x)=x^{2}\sin x^{2}$

$f(x)=\frac{x+1}{1+x^{2}}$

$f(x)=\frac{1+x^{3}}{1+x}$

$f(x)=1-(\ln x)^{2}$

Correct answer:

$f(x)=\frac{1+x^{3}}{1+x}$

Explanation:

A removeable discontinuity occurs whenever there is a hole in a graph that could be fixed (or "removed") by filling in a single point. Put another way, if there is a removeable discontinuity at x=a , then the limit as approaches exists, but the value of f(a) does not.

For example, the function $f(x)=\frac{1+x^3}{1+x}$ contains a removeable discontinuity at x=-1 . Notice that we could simplify f(x) as follows:

$f(x)=\frac{1+x^3}{1+x}=\frac{(1+x)(x^2-x+1)}{1+x}=x^{2}-x+1$ , where $x\neq -1$ .

Thus, we could say that $\lim_{x\rightarrow -1}\frac{1+x^3}{1+x}=\lim_{x\rightarrow -1}x^2-x+1=(-1)^2-(-1)+1=3$ .

As we can see, the limit of f(x) exists at x=-1 , even though f(-1) is undefined.

What this means is that f(x) will look just like the parabola with the equation $x^{2}-x+1$ EXCEPT when x=-1 , where there will be a hole in the graph. However, if we were to just define f(-1)=3 , then we could essentially "remove" this discontinuity. Therefore, we can say that there is a removeable discontinuty at x=-1 .

The functions

$f(x)=\frac{x}{1-x^{2}}$ , and

$f(x)=1-(\ln x)^{2}$

have discontinuities, but these discontinuities occur as vertical asymptotes, not holes, and thus are not considered removeable.

The functions

$f(x)=x^{2}\sin x^{2}$ and $f(x)=\frac{x+1}{1+x^{2}}$ are continuous over all the real values of ; they have no discontinuities of any kind.

The answer is

$f(x)=\frac{1+x^{3}}{1+x}$ .

Report an Error

View AP Calculus AB Tutors

Magdy
Certified Tutor

Cairo University, Egypt, Bachelor of Science, Electrical Engineering. New Mexico State University-Main Campus, Doctor of Phil...

View AP Calculus AB Tutors

Emily
Certified Tutor

University of Michigan-Ann Arbor, Bachelor of Science, Public Health.

View AP Calculus AB Tutors

Keith
Certified Tutor

McGill University, Bachelor, Mathematics.

All AP Calculus AB Resources

3 Diagnostic Tests 164 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

ISEE Tutors in Philadelphia, Physics Tutors in San Francisco-Bay Area, MCAT Tutors in Seattle, MCAT Tutors in Atlanta, Statistics Tutors in Houston, Reading Tutors in Houston, French Tutors in Philadelphia, Biology Tutors in Denver, LSAT Tutors in Miami, Spanish Tutors in New York City

Popular Courses & Classes

SSAT Courses & Classes in Houston, GRE Courses & Classes in Houston, LSAT Courses & Classes in Houston, GRE Courses & Classes in Boston, ISEE Courses & Classes in Miami, ISEE Courses & Classes in Boston, SAT Courses & Classes in Phoenix, GMAT Courses & Classes in Houston, SSAT Courses & Classes in Miami, GMAT Courses & Classes in New York City

Popular Test Prep

ISEE Test Prep in Houston, LSAT Test Prep in Chicago, GRE Test Prep in Seattle, GMAT Test Prep in Philadelphia, ISEE Test Prep in Boston, SAT Test Prep in Washington DC, GRE Test Prep in Miami, SSAT Test Prep in Washington DC, ACT Test Prep in Los Angeles, ISEE Test Prep in Washington DC

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

AP Calculus AB : AP Calculus AB

Study concepts, example questions & explanations for AP Calculus AB

All AP Calculus AB Resources

Example Questions

Example Question #45 : Interpretations And Properties Of Definite Integrals

Example Question #21 : Basic Properties Of Definite Integrals (Additivity And Linearity)

Example Question #22 : Basic Properties Of Definite Integrals (Additivity And Linearity)

Example Question #23 : Basic Properties Of Definite Integrals (Additivity And Linearity)

Example Question #24 : Basic Properties Of Definite Integrals (Additivity And Linearity)

Example Question #21 : Basic Properties Of Definite Integrals (Additivity And Linearity)

Example Question #51 : Interpretations And Properties Of Definite Integrals

Example Question #21 : Basic Properties Of Definite Integrals (Additivity And Linearity)

Example Question #52 : Interpretations And Properties Of Definite Integrals

Example Question #1 : Continunity As A Property Of Functions

All AP Calculus AB Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: