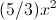Call Now to Set Up Tutoring:

(888) 888-0446

AP Calculus AB : AP Calculus AB

Study concepts, example questions & explanations for AP Calculus AB

Create An Account

All AP Calculus AB Resources

3 Diagnostic Tests 164 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #5 : Understanding The Limiting Process.

Find the derivative of

$f(x)=4(x^{3}-2x+11)(x-2)$

Possible Answers:

$4(3x^{2}-2)$

$3x^{2}-8x+15$

24x-2

$4x^{4}-8x^{3}-8x^{2}+60x-22$

$f'(x)=16x^{3}-24x^{2}-16x+60$

Correct answer:

$f'(x)=16x^{3}-24x^{2}-16x+60$

Explanation:

The answer is $f'(x)=16x^{3}-24x^{2}-16x+60$ . It is easy to solve if we multiply everything together first before taking the derivative.

$f(x)=4(x^{3}-2x+11)(x-2)$

$f(x)=4(x^{4}-2x^{3}+-2x^{2}+4x+11x-22)$

$f(x)=4x^{4}-8x^{3}-8x^{2}+60x-22$

$f'(x)=16x^{3}-24x^{2}-16x+60$

Report an Error

Example Question #4 : Calculus 3

Find $\frac{d^{2}y}{dx^{2}}$ if y^2-x^2 = 4 .

Possible Answers:

$\frac{x^2-4}{\sqrt{x^2+4}}$

$\frac{x^2}{(x^2-4)^\frac{3}{2}}$

$\frac{x^2+4}{(x^2-4)^\frac{3}{2}}$

$\frac{4}{(x^{2}+4)^{\frac{3}{2}}}$

$\frac{x}{\sqrt{4+x^2}}$

Correct answer:

$\frac{4}{(x^{2}+4)^{\frac{3}{2}}}$

Explanation:

We will have to find the first derivative of with respect to using implicit differentiation. Then, we can find $\frac{d^{2}y}{dx^{2}}$ , which is the second derivative of with respect to .

$\frac{d}{dx}[y^2-x^2]=\frac{d}{dx}[4]$

We will apply the chain rule on the left side.

$\frac{d}{dx}[y^2]\cdot \frac{dy}{dx}-\frac{d}{dx}[x^2]=0$

$2y\cdot \frac{dy}{dx}-2x=0$

We now solve for the first derivative with respect to .

$\frac{dy}{dx}=\frac{x}{y}$

In order to get the second derivative, we will differentiate $\frac{x}{y}$ with respect to . This will require us to employ the Quotient Rule.

$\frac{d}{dx}\frac{dy}{dx}=\frac{d^{2}y}{dx^{2}}=\frac{d}{dx}[\frac{x}{y}]=\frac{y\cdot \frac{d}{dx}[x]-x\cdot \frac{d}{dx}[y]}{y^{2}} =\frac{y\cdot 1-x\cdot \frac{dy}{dx}}{y^{2}}$

We will replace $\frac{\mathrm{d}y }{\mathrm{d} x}$ with $\frac{x}{y}$ .

$\frac{y-x(\frac{x}{y})}{y^{2}}=\frac{y^{2}-x^{2}}{y^{3}}$

But, from the original equation, $y^{2}-x^{2}=4$ . Also, if we solve for , we obtain $y = (4+x^{2})^{\frac{1}{2}}$ .

$\frac{d^{2}y}{dx^{2}}=\frac{y^{2}-x^{2}}{y^{3}}=\frac{4}{(x^{2}+4)^{\frac{3}{2}}}$

The answer is $\frac{4}{(x^{2}+4)^{\frac{3}{2}}}$ .

Report an Error

Example Question #4 : Understanding The Limiting Process.

Differentiate f(x)=5x^3 .

Possible Answers:

15x^4

8x^2

(5/3)x^2

15x^2

15x^3

Correct answer:

15x^2

Explanation:

Using the power rule, multiply the coefficient by the power and subtract the power by 1.

f(x)=5x^3

$f'(x)=5*3(x^{3-1})$

f'(x)=15x^2

Report an Error

Example Question #5 : Understanding The Limiting Process.

Differentiate $f(x)=\frac{1}{x^2}$ .

Possible Answers:

2ln(x^2)

$\frac{1}{x^3}$

$\frac{-2}{x^3}$

$\frac{-2}{x}$

ln(x^2)

Correct answer:

$\frac{-2}{x^3}$

Explanation:

Use the product rule:

$f(x)=\frac{1}{x^2}= x^{-2}$

$f'(x)=-2*1(x^{-2-1})= {-2}*{x^{-3}}= \frac{-2}{x^3}$

Report an Error

Example Question #6 : Understanding The Limiting Process.

Differentiate: f(x)=(5x-3)(2x+1)

Possible Answers:

10x^2-x-3

20x-1

20x+1

Correct answer:

20x-1

Explanation:

Use the product rule to find the derivative of the function.

f(x)=(5x-3)(2x+1)

f'(x)= (5x-3)*2+(2x+1)*5

f'(x)= 10x-6+10x+5=20x-1

Report an Error

Example Question #7 : Understanding The Limiting Process.

Differentiate: $y=e^{x^2}$

Possible Answers:

$2x^3e^{x^3}$

2e^x

$2e^{x^2}$

$2xe^{x^2}$

Correct answer:

$2xe^{x^2}$

Explanation:

The derivative of any function of e to any exponent is equal to the function multiplied by the derivative of the exponent.

$f'(x)=e^{x^2}*2x$

Report an Error

Example Question #8 : Understanding The Limiting Process.

Find the second derivative of $y=ln(\frac{x^2}{x^2+1})$ .

Possible Answers:

$\frac{2x}{x^4+x^2}$

$\frac{2}{x^3+x}$

$\frac{-2}{(x^3+x)^2}$

$\frac{-2(3x^2+1)}{(x^3+x)^2}$

Correct answer:

$\frac{-2(3x^2+1)}{(x^3+x)^2}$

Explanation:

y=ln(x^2)-ln(x^2+1)

$y'= \frac{1}{x^2}*2x-\frac{1}{x^2+1}*2x$

$\frac{2x}{x^2}-\frac{2x}{x^2+1}= \frac{2x^3+2x-2x^3}{x^2*(x^2+1)}= \frac{2x}{x^4+x^2}$

Factoring out an x gives you $\frac{2}{x^3+x}$ .

$y''=2(x^3+x)^{-1}=-2(x^3+x)^{-2}*(3x^2+1)=\frac{-2(3x^2+1)}{(x^3+x)^2}$

Report an Error

Example Question #191 : Derivative Review

What is the derivative of $(2+3cos(3x))^\pi$ ?

Possible Answers:

$3\pi(2+cos(3x))^{\pi-1}cos(3x)$

$3\pi(2+cos(3x))^{\pi-1}sin(3x)$

$-3\pi(2+cos(3x))^{\pi-1}sin(3x)$

$-3\pi(2+cos(3x))^{\pi-1}cos(3x)$

$-3\pi(2+cos(3x))^{\pi-1}$

Correct answer:

$-3\pi(2+cos(3x))^{\pi-1}sin(3x)$

Explanation:

Need to use the power rule which states: $\frac{d}{dx}u^n=nu^{n-1}\frac{du}{dx}$

In our problem $\frac{du}{dx}=-3sin(3x)$

Report an Error

Example Question #11 : Understanding The Limiting Process.

Consider:

$f(x) = x^{99} - x^{66}$

The 99th derivative of f(x) is:

Possible Answers:

99! + 66!

99!

99! - 66!

99!(x)

Correct answer:

99!

Explanation:

For $f(x) = x^{n}$ , the nth derivative is . As an example, consider $f(x) = x^{3}$ . The first derivative is $3x^{2}$ , the second derivative is $3*2x\: (or\: 6x)$ , and the third derivative is $3*2*1,\: or \: 3!$ . For the question being asked, the 99th derivative of $x^{99}$ would be 99! . The 66th derivative of $x^{66}$ would be 66! , and any higher derivative would be zero, since the derivative of any constant is zero. Thus, for the given function, the 99th derivative is 99! .

Report an Error

Example Question #1131 : Ap Calculus Ab

Consider the function $f(x) = 4x^{2} - sin(x) - 10x$ .

Which of the following is true when $x = \pi$ ?

Possible Answers:

f(x) > 0 and is increasing and concave down.

f(x) > 0 and is decreasing and concave up.

f(x) > 0 and is increasing and concave up.

f(x) < 0 and is increasing and concave up.

f(x) < 0 and is increasing and concave down.

Correct answer:

f(x) > 0 and is increasing and concave up.

Explanation:

$f(\pi ) = 4\pi^{2} - sin(\pi ) - 10\pi > 0$

$f'(\pi ) = 8\pi - cos(\pi) -10 > 0$ , meaning f(x) is increasing when x = $\pi$ .

$f''(\pi ) = 8 + sin(\pi ) > 0$ , meaning f(x) is concave up when x = $\pi$ .

Report an Error

View AP Calculus AB Tutors

Garth
Certified Tutor

View AP Calculus AB Tutors

Satweka
Certified Tutor

The University of Texas at Dallas, Master of Science, Biomedical Engineering.

View AP Calculus AB Tutors

George
Certified Tutor

Northern Arizona University, Bachelors, Chemistry. Purdue University-Main Campus, PHD, Chemistry.

All AP Calculus AB Resources

3 Diagnostic Tests 164 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

ACT Tutors in Dallas Fort Worth, Algebra Tutors in Miami, Chemistry Tutors in Chicago, Biology Tutors in New York City, Reading Tutors in Washington DC, Math Tutors in San Francisco-Bay Area, Math Tutors in Miami, SAT Tutors in Boston, Statistics Tutors in Philadelphia, Computer Science Tutors in Miami

Popular Courses & Classes

MCAT Courses & Classes in Los Angeles, LSAT Courses & Classes in Miami, ACT Courses & Classes in New York City, ACT Courses & Classes in Philadelphia, GMAT Courses & Classes in Washington DC, Spanish Courses & Classes in Denver, ACT Courses & Classes in Dallas Fort Worth, SAT Courses & Classes in Houston, Spanish Courses & Classes in Boston, Spanish Courses & Classes in Dallas Fort Worth

Popular Test Prep

GMAT Test Prep in Los Angeles, ISEE Test Prep in Philadelphia, LSAT Test Prep in Atlanta, GMAT Test Prep in Washington DC, LSAT Test Prep in San Francisco-Bay Area, GMAT Test Prep in Denver, ACT Test Prep in Houston, SSAT Test Prep in San Francisco-Bay Area, GMAT Test Prep in Seattle, MCAT Test Prep in Los Angeles

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

AP Calculus AB : AP Calculus AB

Study concepts, example questions & explanations for AP Calculus AB

All AP Calculus AB Resources

Example Questions

Example Question #5 : Understanding The Limiting Process.

Example Question #4 : Calculus 3

Example Question #4 : Understanding The Limiting Process.

Example Question #5 : Understanding The Limiting Process.

Example Question #6 : Understanding The Limiting Process.

Example Question #7 : Understanding The Limiting Process.

Example Question #8 : Understanding The Limiting Process.

Example Question #191 : Derivative Review

Example Question #11 : Understanding The Limiting Process.

Example Question #1131 : Ap Calculus Ab

All AP Calculus AB Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: