All Algebra II Resources
Example Questions
Example Question #5 : Experiment Design And Identifying Bias
A marketer is piloting a set of new advertisement slogans--a potential replacement for her company’s old slogans--to determine the new slogans’ effectiveness at raising the number of clicks her ads receive. She partners with a social media company to test the slogans by targeting 1,000 random social media users each day with the new slogans and targeting 1,000 different random users each day with the old slogans.
Which of the following is the control group?
Users targeted with the new slogans
Users targeted with the old slogans
The social media company
The researcher
Users targeted with the old slogans
The control group in an experiment does not receive the experimental treatment, but resembles the group receiving the experimental treatment. Thus, the dependent variable associated with the control group is not affected by the independent variable in the experiment. This allows the researcher to compare the effect of the experimental treatment on the experimental group with the effect of no treatment, making the effect of the treatment easier to verify.
Example Question #6 : Experiment Design And Identifying Bias
A marketer is piloting a set of new advertisement slogans--a potential replacement for her company’s old slogans--to determine the new slogans’ effectiveness at raising the number of clicks her ads receive. She partners with a social media company to test the slogans by targeting 1,000 random social media users each day with the new slogans and targeting 1,000 different random users each day with the old slogans.
Which of the following is the experimental group?
Users targeted with the new slogans
The researcher
Users targeted with the old slogans
The social media company
Users targeted with the new slogans
The experimental group in an experiment receives the experimental treatment. The dependent variable associated with the experimental group is affected by the independent variable in the experiment, while the dependent variable associated with the control group is not.
Example Question #10 : Experiment Design And Identifying Bias
A marketer is piloting a set of new advertisement slogans--a potential replacement for her company’s old slogans--to determine the new slogans’ effectiveness at raising the number of clicks her ads receive. She partners with a social media company to test the slogans by targeting 1,000 random social media users each day with the new slogans and targeting 1,000 different random users each day with the old slogans. When the study ends, she compares the click activity on ads with each type of slogan and concludes that the new slogans are effective.
The results are represented in the table below:

Is her conclusion correct?
Yes. The new ads have more clicks than the old ads.
No. The old ads have fewer clicks than the new ads.
No. The results are not statistically significant.
Yes. The results are statistically significant.
No. The results are not statistically significant.
A statistically significant result of an experiment is one in which a change in the experimental group’s dependent variable is attributable to a change in the independent variable. In other words, a statistically significant result in a well designed experiment is one that is large enough in scale that it is unlikely to be a result of mere chance. In the table provided, the difference between the total ad clicks resulting from each of the slogan types is minuscule--a difference of only 3 clicks out of over 2,000 for each type. This suggests that the results may simply have been the result of chance, since the difference in total clicks is so small in scale that it is difficult to clearly attribute to the change in slogan types.
Example Question #5181 : Algebra Ii
A student wants to find out whether mothers in his city support a local initiative to redesign the city’s largest park. He decides to conduct a poll on this question by calling the home phone numbers of all 200 students in his private high school, asking to speak to their mothers, and recording their responses as YES, NO or NO PREFERENCE in a chart. He doesn’t have time to make 400 calls, so he enlists three friends, who are also students at his school, to help make calls and record answers.
100 calls are not answered, and during 50 calls no mothers are home. The remaining 250 calls successfully reach mothers: 200 of the 250 calls are recorded as YES, 25 are recorded as NO and 25 are recorded as NO PREFERENCE. The student concludes that most mothers in the city support the initiative.
Which of the following forms of bias does NOT appear in this study?
Measurement bias
Interviewer bias
Response bias
Sampling bias
Measurement bias
Sampling bias occurs when populations are included or excluded from study participation in a way that systematically affects the sample’s representativeness of the population the researcher seeks to gain knowledge about. Given the small population of students at the high school, it is highly unlikely that all mothers in the city are represented in the sample; and given that the high school is both small and private, it is unlikely that the sample is representative of all mothers in the city. Interviewer bias occurs when there is a possibility that an interviewer may behave in ways that consciously or unconsciously influence respondents to give answers skewed towards the interviewer’s perspective or interests. Response bias occurs when respondents consciously or subconsciously give responses they believe the interviewer wants to hear. Interviewer and response bias may result from the fact that the students attend the same schools that the respondents’ children attend, and the fact that the small size of the high school increases the likelihood of personal connections existing between the students and the respondents. The description provides no evidence of measurement bias, or systematic incorrect measurement, in this study.
Example Question #93 : Probability
The mean of the following numbers is 13. Solve for x.
18, 15, 10, 8, x
15
14
13
12
14
where n equals the number of events.
Example Question #94 : Probability
On 3 exams, Willow has an average score of 95 points. Her lowest score was an 90. If this score is dropped, what is her new average?
98
97.5
100
96
97.5
To answer this question, you must first calculate Willow's total points from the 3 exams. The total points will be equal to 3 times the original average:
95*3=285
Now, if the 90 is removed, his new total will be:
285-90=195
With the score dropped, her new total number of exams is 2. Therefore, the new average is:
Example Question #91 : Probability
The ages of the students at Rosa Parks High School are normally distributed with a mean of 15.5 and a standard deviation of 0.6 years.
What is the proportion of students that are older than 16.2 years old?
5%
1%
0%
2.5%
2.5%
This question relates to the 68−95−99.7 rule of normal distribution. We know that 95% of the data are within 2 standard deviations from the mean.
In this case this means that 95% of the students are between
15.5−2⋅0.6 and 15.5+2⋅0.5
15−1.2 and 15+1.2
13.8 and 16.2
Therefore we have 5% of the students that are outside of this range. Since the normal distribution is symmetric, the proportion of students below 13.8 is the same as the proportion of students above 16.2.
Thus the right answer is one half of 5%, or 2.5%.
2.5% of the students are older than 16.2 years old.
Example Question #4 : Mean, Standard Deviation, And Normal Distribution
The ages of the students at Central Universityl are normally distributed with a mean of 23.5 and a standard deviation of 2.5 years.
What is the proportion of students that are younger than 18.5 years old?
1%
5%
0%
2.5%
2.5%
This question relates to the 68−95−99.7 rule of normal distribution. We know that 95% of the data are within 2 standard deviations from the mean.
In this case this means that 95% of the students are between
23.5−2⋅2.5 and 23.5+2⋅2.5
23.5-5 and 23.5+5
18.5 and 28.5
Therefore we have 5% of the students that are outside of this range. Since the normal distribution is symmetric, the proportion of students below 18.5 is the same as the proportion of students above 28.5.
Thus the right answer is half of 5% or 2.5%.
Example Question #5221 : Algebra Ii
Find the standard deviation of the following set of numbers:
To begin, we must remember the formula for standard deviation:
where 


Now we can determine the value for our summation for each number in the set:
Looking at our equation for standard variation, now all we must do is sum all of the values above, divide by N, and take the square root:
Example Question #3 : Mean, Standard Deviation, And Normal Distribution
The formula for standard deviation is the following:

Where,

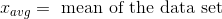
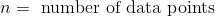
Five students took a test and recieved the following grades: 




None of the other answers.
The first step in solving for standrd deviation is to find the mean of the data set.
For this problem:

Now we can evaluate the summation:
Now we can rewrite the standard deviation expression:
There are 5 data points, so n = 5
All Algebra II Resources

































