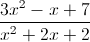Remember that the least common denominator is the smallest number such that all fractions' denominators divide it evenly.

Always start with the largest number. In this case, it is 12. 3, 4, 6, and 12 all divide evenly into 12, but 8 does not. Think of the next multiple of the largest number. In this case, 24. Here we see that 3, 4, 6, 8, and 12 all divide 24 evenly. Thus, our least common denominator is 24.

To simplify the expression, we must find the common denominator, which in this case is 

Note that when we distribute the x, we get the denominator of the third term, .

Now, we multiply each term by the LCD divided by itself:

Which, after some canceling, becomes

Now that all of the terms have the same denominator, we can add their numerators together:

In order to determine the least common denominator, multiply all the uncommon denominators together. 

Use the distributive property to simplify these terms.

The least common denominator is:  

In order to continue to simplify this problem, we will need to multiply both denominators together in order to simplify the numerators.

Multiply both of the denominators by using the FOIL method.

Simplify this expression.

The least common denominator required is:  

Be careful not to continue and solve the problem!

The answer is:  

Determine the least common denominator by multiplying the denominators together.

Multiply the first two terms together.

Multiply this quantity with the third term.

Use the FOIL method to expand this expression.

Simplify and combine like terms.

The answer is:  

In order to determine the least common denominator, we will need to use the FOIL method to expand the denominators.

Multiply the terms.

Combine like-terms.

The answer is:  

In order to determine the least common denominator, we will need to multiply both denominators together.  Be careful not to mix up the denominators as similar entities.

Do not solve the problem.  

The answer is:  

The least common denominator is the term that is both divisible by all denominators and do not have common denominators smaller than this term.

Notice that both denominators can share a .  We can simply change the first denominator to  by multiplying an x-term.

For the second denominator, notice that we can change the three to a nine, similar to the first denominator by multiplying a three.

Since these terms are common and is the least possible term, this is the least common denominator.

The answer is:  

In order to determine the least common denominator, we will need to break up both denominator with their simplest forms.

Notice that both of the values share an  term.  The first expression lacks a two coefficient, and the second expression lacks an  term.

This means that the LCD will be:  

Simplify this expression by distribution.

The answer is:  

This is a more complicated form of

Find the least common denominator (LCD) and convert each fraction to the LCD, then add the numerators.  Simplify as needed.

which is equivalent to

Simplify to get