All Algebra II Resources
Example Questions
Example Question #5 : Completing The Square
Solve the following equation by completing the square. Use a calculator to determine the answer to the closest hundredth.


No solution



To solve by completing the square, you should first take the numerical coefficient to the “right side” of the equation:
Then, divide the middle coefficient by 2:
Square that and add it to both sides:
Now, you can easily factor the quadratic:

Take the square root of both sides:
Finish out the solution:
Example Question #6 : Completing The Square
Solve the following equation by completing the square. Use a calculator to determine the answer to the closest hundredth.
No solution





To solve by completing the square, you should first take the numerical coefficient to the “right side” of the equation:

Then, divide the middle coefficient by 2:

Square that and add it to both sides:
Now, you can easily factor the quadratic:
Take the square root of both sides:
Finish out the solution:
Example Question #7 : Completing The Square
Solve the following equation by completing the square. Use a calculator to determine the answer to the closest hundredth.
No solution





To solve by completing the square, you should first take the numerical coefficient to the “right side” of the equation:
Then, divide the middle coefficient by 2:
Square that and add it to both sides:
Now, you can easily factor the quadratic:
Take the square root of both sides:
Finish out the solution:
Example Question #1 : Completing The Square
Solve the following equation by completing the square. Use a calculator to determine the answer to the closest hundredth.
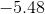


No solution

No solution
To solve by completing the square, you should first take the numerical coefficient to the “right side” of the equation:
Then, divide the middle coefficient by 2:
Square that and add it to both sides:
Now, you can easily factor the quadratic:
Your next step would be to take the square root of both sides. At this point, however, you know that you cannot solve the problem. When you take the square root of both sides, you will be forced to take the square root of 
Example Question #9 : Completing The Square
Use completing the square to solve the following equation, simplifying radicals completely:
From the original equation, we add 18 to both sides in order to set up our "completing the square."
To make completing the square sensible, we divide both sides by 2.
We now divide the x coefficient by 2, square the result, and add that to both sides.
Since the right side is now a perfect square, we can rewrite it as a square binomial.
Take the square root of both sides, simplify the radical and solve for x.
Example Question #1 : Completing The Square
Solve the following equation by completing the square:
We start by moving the constant term of the quadratic to the other side of the equation, to set up the "completing the square" format.
Now to make completing the square sensible, we divide boths sides by 2 so that x^2 will not have a coefficient.
Now we can complete the square by dividing the x coefficient by 2 and squaring the result, then adding that result to both sides.
Because the left side is now a perfect square, we can rewrite it as a squared binomial.
Take the square root of both sides, and then solve for x.
Example Question #81 : Solving Quadratic Equations
Solve the following equation by completing the square.
Starting with the original equation, we move the constant term of the quadratic over to the other side, so we can set up our "completing the square."
Since the x^2 coefficient is already 1, we don't have to do any division. We can go straight to completing the square by dividing the x coefficient by 2, squaring the result, and adding that result to both sides.
Since the left side is now a perfect square, we can rewrite it as a squared binomial.
Now take the square root of both sides and solve for x.
Example Question #82 : Solving Quadratic Equations
Rewrite the follow parabola equation in vertex form:
We start by moving the constant term of the quadratic over to the other side of the equation, in order to set up our "completing the square" form.
Next we divide both sides by 4 so that the x^2 coefficient will be 1. That will allow us to complete the square.
Now we are ready to complete the square. We divide the x coefficient by 2, square the result, and add that result to both sides.
Because the right side is now a perfect square, we can rewrite it as a squared binomial.
To finish, all we have to do now is solve for y. We'll subtract 5 to both sides, then multiply by 4.
Example Question #83 : Solving Quadratic Equations
Solve by completing the square.
The first step is to make sure the x2 term has a coefficient of 1. Since we have that, we move onto the next step.
Next, move the "loose" number over to the other side.
Now divide the coefficient of the x term by 2 (don't forget the sign!). Add the square of this number to both sides.
Simplify:
Now the left side of the equation can be simplified to a squared factor. The factor that will be squared is going to be x plus the original x coefficient divided by 2 as we calculated above.
Take the square root of both sides:
Solve for x:
Example Question #231 : Quadratic Equations And Inequalities
Using the above equation, what should the next step look like when completing the square?
The first step when completing the square is to move the constant to the other side of the equation by subtracting from both sides. Don't forget the sign!
Certified Tutor
All Algebra II Resources





























































































































































