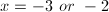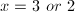Call Now to Set Up Tutoring:

(888) 888-0446

Algebra II : Quadratic Equations and Inequalities

Study concepts, example questions & explanations for Algebra II

Create An Account

All Algebra II Resources

10 Diagnostic Tests 630 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Using Foil

Solve the equation for .

$\small \frac{1}{x}=\frac{x+1}{6}$

Possible Answers:

$\small x=3\ or\ -2$

$\small x=-3\ or\ -2$

$\small x=-3\ or\ 2$

$\small x=3\ or\ 2$

Correct answer:

$\small x=-3\ or\ 2$

Explanation:

$\small \small \frac{1}{x}=\frac{x+1}{6}$

Cross multiply.

$\small 6=x(x+1)$

$\small 6=x^2+x$

Set the equation equal to zero.

$\small 0=x^2+x-6$

Factor to find the roots of the polynomial.

3*-2=-6 and 3+(-2)=1

$\small 0=(x+3)(x-2)$

$\small 0=x+3; x=-3$

$\small 0=x-2; x=2$

Report an Error

Example Question #1 : Quadratic Equations And Inequalities

$Expand \; (5x^2 +x + 1)(3x-2)$

Possible Answers:

15 x^2-6 x-2

15 x^3-7 x^2+x-2

8x^3-7 x^2+x-2

15 x^3+7 x^2-x-2

Correct answer:

15 x^3-7 x^2+x-2

Explanation:

$Multiply \; (3 x-2) (5 x^2+x+1)\; using \; a \; grid$

$Answer: \; 15 x^3-7 x^2+x-2$

Report an Error

Example Question #2 : Simplifying And Expanding Quadratics

Solve the equation for :

$\frac{x}{2}=\frac{-1}{x+3}$

Possible Answers:

x=1, x=2

x=0

x=1

x=-1, x=-2

x=1, x=0

Correct answer:

x=-1, x=-2

Explanation:

$\frac{x}{2}=\frac{-1}{x+3}$

1. Cross multiply:

$x^{2}+3x=-2$

2. Set the equation equal to :

$x^{2}+3x+2=0$

3. Factor to find the roots:

(x+2)(x+1)=0

x+2=0 , so x=-2

x+1=0 , so x=-1

Report an Error

Example Question #3 : Simplifying And Expanding Quadratics

If you were to solve $x^{2}+8x+9=0$ by completing the square, which of the following equations in the form (x+f)^2=g do you get as a result?

Possible Answers:

(x+8)^2=16

(x+8)^2=64

(x+4)^2=25

(x+4)^2=7

(x+4)^2=16

Correct answer:

(x+4)^2=7

Explanation:

When given a quadratic in the form x^2+bx+c=0 and told to solve by completing the square, we start by subtracting from both sides. In this problem is equal to , so we start by subtracting from both sides:

x^2+8x=-9

To complete the square we want to add a number to each side which yields a polynomial on the left side of the equals sign that can be simplified into a squared binomial (x+d)^2 . This number is equal to $(\frac{b}{2})^2$ . In this problem is equal to , so:

$(\frac{b}{2})^2=(\frac{8}{2})^2=4^2=16$

We add to both sides of the equation:

x^2+8x+16=-9+16

We then factor the left side of the equation into binomial squared form and combine like terms on the right:

(x+4)^2=7

Report an Error

Example Question #1 : Understanding Quadratic Equations

If you were to solve $x^{2}+4x-5=0$ by completing the square, which of the following equations in the form (x+f)^2=g do you get as a result?

Possible Answers:

(x+2)^2=5

(x-2)^2=9

(x+2)^2=9

(x+2)^2=21

(x+2)^2=7

Correct answer:

(x+2)^2=9

Explanation:

x^2+4x=5

To complete the square we want to add a number to each side which yields a polynomial on the left side of the equation that can be simplified into a squared binomial (x+d)^2 . This number is equal to $(\frac{b}{2})^2$ . In this problem is equal to , so:

$(\frac{b}{2})^2=(\frac{4}{2})^2=2^2=4$

We add to both sides of the equation:

x^2+4x+4=5+4

We then factor the left side of the equation into binomial squared form and combine like terms on the right:

(x+2)^2=9

Report an Error

Example Question #1 : Simplifying And Expanding Quadratics

Expand:

(4x-1)(-2x+3)

Possible Answers:

$8x^{2}+10x-3$

$-8x^{2}+14x-3$

$-8x^{2}+10x-3$

None of the other answers are correct.

$8x^{2}+14x-3$

Correct answer:

$-8x^{2}+14x-3$

Explanation:

Use the FOIL method, which stands for First, Inner, Outer, Last:

(4x)(-2x)+(4x)(3)+(-1)(-2x)+(-1)(3)

= -8x^2+12x+2x-3

$=-8x^{2}+14x-3$

Report an Error

Example Question #2 : Simplifying And Expanding Quadratics

Multiply: $(x^{2} + 3) (4x - 1)$

Possible Answers:

$4x^{3} +x^{2} -12x - 3$

$4x^{3} + 3$

$4x^{3} -x^{2} +12x - 3$

$4x^{3} - 3$

$4x^{3} -x^{2} -12x + 3$

Correct answer:

$4x^{3} -x^{2} +12x - 3$

Explanation:

$(x^{2} + 3) (4x - 1)$

$= x^{2} (4x - 1) + 3(4x - 1)$

$= x^{2} \cdot 4x - x^{2} \cdot 1 + 3 \cdot 4x - 3 \cdot 1$

$= 4x^{3} - x^{2} + 12x - 3$

Report an Error

Example Question #2 : Simplifying And Expanding Quadratics

Multiply: $(x + 4) (x^{2} -4x + 16)$

Possible Answers:

$x^{3}- 12x - 64$

$x^{3}- 20x + 64$

$x^{3}- 12x + 64$

$x^{3} - 64$

$x^{3} + 64$

Correct answer:

$x^{3} + 64$

Explanation:

$(x + 4) (x^{2} -4x + 16)$

$= x (x^{2} -4x + 16)+ 4 (x^{2} -4x + 16)$

$= x \cdot x^{2} -x \cdot 4x + x \cdot 16+ 4 \cdot x^{2} -4 \cdot 4x + 4 \cdot 16$

$= x^{3} -4x^{2} + 16x+ 4 x^{2} -16x + 64$

$= x^{3} -4x^{2} + 4 x^{2} + 16x -16x + 64$

$= x^{3} + 64$

Report an Error

Example Question #1 : How To Subtract Trinomials

Subtract:

(x^2+15x-3)-(x^2-5x-3)

Possible Answers:

20x

20x+6

x^4+20x^2+6

2x^2+20x+6

20x^2

Correct answer:

20x

Explanation:

When subtracting trinomials, first distribute the negative sign to the expression being subtracted, and then remove the parentheses: (x^2+15x-3)-(x^2-5x-3)=x^2+15x-3-x^2+5x+3

Next, identify and group the like terms in order to combine them: (x^2-x^2)+(15x+5x)+(3-3)=20x .

Report an Error

Example Question #1 : Understanding Quadratic Equations

Evaluate the following:

(x^2+2x-4)(2x+5)

Possible Answers:

2x^3+9x^2+2x+20

2x^3+9x^2+2x-20

2x^3+9x^2+18x-20

4x^3+6x^2+2x-20

Correct answer:

2x^3+9x^2+2x-20

Explanation:

When multiplying this trinomial by this binomial, you'll need to use a modified form of FOIL, by which every term in the binomial gets multiplied by every term in the trinomial. One way to do this is to use the grid method.

You can also solve it piece-by-piece the way it is set up. First, multiply each of the three terms in the trinomail by . Then multiply each of those three terms again, this time by .

$(x^2+2x-4) \times 2x = 2x^3 + 4x^2 - 8x$

$(x^2+2x-4) \times 5 = 5x^2 + 10x - 20$

Finally, you can combine like terms after this multiplication to get your final simplified answer:

2x^3 + 9x^2 +2x-20

Report an Error

View Algebra 2 Tutors

Michael
Certified Tutor

University of California-San Diego, Bachelors, Physics with specialization in Earth Science. University of California-San Die...

View Algebra 2 Tutors

Sharon
Certified Tutor

Tabor College, Bachelor of Science, Mathematics Teacher Education. Tabor College, Masters in Education, Education.

View Algebra 2 Tutors

Gregory
Certified Tutor

Pennsylvania State University-Main Campus, Bachelor of Science, Chemical Engineering. Carnegie Mellon University, Doctor of P...

All Algebra II Resources

10 Diagnostic Tests 630 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

GRE Tutors in Washington DC, Spanish Tutors in San Francisco-Bay Area, Math Tutors in Los Angeles, SSAT Tutors in New York City, Spanish Tutors in Dallas Fort Worth, Reading Tutors in Houston, ISEE Tutors in Chicago, LSAT Tutors in New York City, SSAT Tutors in Chicago, Spanish Tutors in Miami

Popular Courses & Classes

SAT Courses & Classes in Chicago, GRE Courses & Classes in Denver, LSAT Courses & Classes in Seattle, ACT Courses & Classes in Miami, SSAT Courses & Classes in Washington DC, Spanish Courses & Classes in Denver, Spanish Courses & Classes in Phoenix, LSAT Courses & Classes in Phoenix, Spanish Courses & Classes in Atlanta, Spanish Courses & Classes in Washington DC

Popular Test Prep

SAT Test Prep in Washington DC, GMAT Test Prep in Philadelphia, ACT Test Prep in Atlanta, GRE Test Prep in Atlanta, GMAT Test Prep in San Diego, GMAT Test Prep in Denver, GRE Test Prep in Seattle, GMAT Test Prep in Seattle, SAT Test Prep in Phoenix, ACT Test Prep in Miami

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Algebra II : Quadratic Equations and Inequalities

Study concepts, example questions & explanations for Algebra II

All Algebra II Resources

Example Questions

Example Question #1 : Using Foil

Example Question #1 : Quadratic Equations And Inequalities

Example Question #2 : Simplifying And Expanding Quadratics

Example Question #3 : Simplifying And Expanding Quadratics

Example Question #1 : Understanding Quadratic Equations

Example Question #1 : Simplifying And Expanding Quadratics

Example Question #2 : Simplifying And Expanding Quadratics

Example Question #2 : Simplifying And Expanding Quadratics

Example Question #1 : How To Subtract Trinomials

Example Question #1 : Understanding Quadratic Equations

All Algebra II Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: