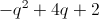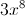Call Now to Set Up Tutoring:

(888) 888-0446

Algebra II : Expressions

Study concepts, example questions & explanations for Algebra II

Create An Account

All Algebra II Resources

10 Diagnostic Tests 630 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #61 : Expressions

Simplify the following expression:

$(2q^{2}+4q+7)-(3q^{2}-5)$

Possible Answers:

$-3q^{2}+12$

$-q^{2}+4q+12$

$-5q^{2}+4q+2$

-q^2+4q+2

Correct answer:

$-q^{2}+4q+12$

Explanation:

This is not a FOIL problem, as we are adding rather than multiplying the terms in parentheses.

Add like terms together:

$2q^{2}-3q^{2}=-1q^{2}=-q^2$

has no like terms.

7-(-5)=12

Combine these terms into one expression to find the answer:

$-q^{2}+4q+12$

Report an Error

Example Question #1 : How To Multiply Polynomials

Simplify the expression.

$x^{5}*x^{16}$

Possible Answers:

The expression cannot be simplified further.

$x^{21}$

$x^{80}$

$x^{11}$

$2x^{16}$

Correct answer:

$x^{21}$

Explanation:

When multiplying exponential components, you must add the powers of each term together.

5+16=21

$x^{5}*x^{16}=x^{21}$

Report an Error

Example Question #1 : How To Multiply Polynomials

$x^{5}y^{17}*x^{2}y^{2}=?$

Possible Answers:

$x^{7}y^{19}$

None of the other answers are correct.

$2x^{2}x^{7}y^{19}$

$x^{2}y^{8}$

$x^{10}y^{34}$

Correct answer:

$x^{7}y^{19}$

Explanation:

When multiplying polynomials, add the powers of each like-termed variable together.

For x: 5 + 2 = 7

For y: 17 + 2 = 19

Therefore the answer is $x^{7}y^{19}$ .

Report an Error

Example Question #62 : Expressions

Simplify the following:

$\frac{x^2-10x+25}{x^2-25}$

Possible Answers:

$\frac{(x-5)(x-5)}{(x-5)(x+5)}$

$\frac{x-5}{x+5}$

This fraction cannot be simplified.

Correct answer:

$\frac{x-5}{x+5}$

Explanation:

$\frac{x^2-10x+25}{x^2-25}$

First we will factor the numerator:

x^2-10x+25=(x-5)(x-5)

Then factor the denominator:

x^2-25=(x+5)(x-5)

We can re-write the original fraction with these factors and then cancel an (x-5) term from both parts:

$\frac{(x-5)(x-5)}{(x-5)(x+5)}=\frac{x-5}{x+5}$

Report an Error

Example Question #1 : Operations With Polynomials

Divide 3x^3+5x^2-x+8 by x^2-1 .

Possible Answers:

$3x+5-\frac{2x+13}{x^2-1}$

$3x+5+\frac{x^2+1}{2x-13}$

$x^2-1-\frac{3x+5}{2x+13}$

$2x+13+\frac{3x+5}{x^2-1}$

$3x+5+\frac{2x+13}{x^2-1}$

Correct answer:

$3x+5+\frac{2x+13}{x^2-1}$

Explanation:

First, set up the division as the following:

$\begin{array}{*2r @{\hskip\arraycolsep}c@{\hskip\arraycolsep} *4r} & && & & & \\ \cline{3-7} x^2 & -1 &\big)& 3x^3 & 5x^2 & -x & 8 \end{array}$

Look at the leading term x^2 in the divisor and 3x^3 in the dividend. Divide 3x^3 by x^2 gives ; therefore, put on the top:

$\begin{array}{*2r @{\hskip\arraycolsep}c@{\hskip\arraycolsep} *4r} & && 3x & & & \\ \cline{3-7} x^2 & -1 &\big)& 3x^3 & 5x^2 & -x & 8 \end{array}$

Then take that and multiply it by the divisor, x^2-1 , to get 3x^3-3x . Place that 3x^3-3x under the division sign:

$\begin{array}{*2r @{\hskip\arraycolsep}c@{\hskip\arraycolsep} *4r} & && 3x & & & \\ \cline{3-7} x^2 & -1 &\big)& 3x^3 & 5x^2 & -x & 8 \\ & && 3x^3 & -3x \end{array}$

Subtract the dividend by that same 3x^3-3x and place the result at the bottom. The new result is 5x^2+2x+8 , which is the new dividend.

$\begin{array}{*2r @{\hskip\arraycolsep}c@{\hskip\arraycolsep} *4r} & && 3x & & & \\ \cline{3-7} x^2 & -1 &\big)& 3x^3 & 5x^2 & -x & 8 \\ & && 3x^3 & -3x \\ \cline{4-7} & && & 5x^2 & 2x & 8 \end{array}$

Now, 5x^2 is the new leading term of the dividend. Dividing 5x^2 by x^2 gives 5. Therefore, put 5 on top:

$\begin{array}{*2r @{\hskip\arraycolsep}c@{\hskip\arraycolsep} *4r} & && 3x & 5 & & \\ \cline{3-7} x^2 & -1 &\big)& 3x^3 & 5x^2 & -x & 8 \\ & && 3x^3 & -3x \\ \cline{4-7} & && & 5x^2 & 2x & 8 \end{array}$

Multiply that 5 by the divisor and place the result, 5x^2-5 , at the bottom:

Perform the usual subtraction:

Therefore the answer is 3x+5 with a remainder of 2x+13 , or $3x+5+\frac{2x+13}{x^2-1}$ .

Report an Error

Example Question #66 : Expressions

Simplify the expression:

$\frac{x^{2}y^{15}z^{-2}}{x^{5}y^{4}}$

Possible Answers:

The fraction cannot be simplified further.

$\frac{y^{11}}{x^{3}z^{2}}$

$\frac{y^{12}}{x^{2}z^{2}}$

$\frac{x^{2}y^{2}}{z^{2}}$

$\frac{y^{9}}{z^{2}}$

Correct answer:

$\frac{y^{11}}{x^{3}z^{2}}$

Explanation:

When dividing polynomials, subtract the exponent of the variable in the numberator by the exponent of the same variable in the denominator.

If the power is negative, move the variable to the denominator instead.

First move the negative power in the numerator to the denominator:

$\frac{x^{2}y^{15}}{x^{5}y^{4}z^{2}}$

Then subtract the powers of the like variables:

$\frac{y^{11}}{x^{3}z^{2}}$

Report an Error

Example Question #2 : Simplifying Expressions

Simplify:

$x^{3}\times{x^{4}}+x$

Possible Answers:

$3x^{8}$

$x^{13}$

$x^{7}+x$

$x^{8}$

$x^{12} + x$

Correct answer:

$x^{7}+x$

Explanation:

$x^{m}\times{x^{n}} = x^{m+n}$ . However, $x^{7}+x$ cannot be simplified any further because the terms have different exponents.

(Like terms are terms that have the same variables with the same exponents. Only like terms can be combined together.)

Report an Error

Example Question #21 : Simplifying Expressions

Simplify:

$\left (\frac{6x^{2}}{t} \right )^{-3}$

Possible Answers:

$\frac{216 t^{3} } { x^{6} }$

$\frac{18 t^{3} } {x^{6} }$

$\frac{t^{3} } { 216 x^{6} }$

$\frac{t^{3} } { 216 x^{5} }$

$\frac{t^{3} } {18 x^{6} }$

Correct answer:

$\frac{t^{3} } { 216 x^{6} }$

Explanation:

Apply the laws of exponents as follows:

$\left (\frac{6x^{2}}{t} \right )^{-3}$

$= \left (\frac{t} {6x^{2}}\right )^{3}$

$= \frac{t^{3} } { \left ( 6x^{2} \right ) ^{3} }$

$= \frac{t^{3} } { 6 ^{3} \left ( x^{2} \right ) ^{3}}$

$= \frac{t^{3} } { 216 \left ( x^{2 \cdot 3} \right ) }$

$= \frac{t^{3} } { 216 x^{6} }$

Report an Error

Example Question #68 : Expressions

Simplify the expression:

$\frac{17}{x^{2}-x-6} + \frac{x+5}{x-3}$

Possible Answers:

$\frac{x^{2}+7x+27}{x-3}$

$\frac{x^{2}+7x+27}{x^{2}-x-6}$

$\frac{x^{2}+7x+10}{x^{2}-x-6}$

$\frac{x^{2}+7x+27}{x+2}$

$\frac{x+22}{x^{2}-x-6}$

Correct answer:

$\frac{x^{2}+7x+27}{x^{2}-x-6}$

Explanation:

$\frac{17}{x^{2}-x-6} + \frac{x+5}{x-3}$

1. Factor $x^{2}-x-6$

(x+2)(x-3)

***notice that the two fractions now share a factor in the denominator***

$\frac{17}{(x+2)(x-3)} + \frac{x+5}{x-3}$

2. Create a common denominator between the two terms

$\frac{17}{(x+2)(x-3)} + \frac{(x+5)(x+2)}{(x-3)(x+2)}$

3. Simplify

$=\frac{17}{x^{2}-x-6} + \frac{x^{2}+7x+10}{x^{2}-x-6}$

$=\frac{17 +x^{2}+7x+10}{x^{2}-x-6}$

$=\frac{x^{2}+7x+27}{x^{2}-x-6}$

Report an Error

Example Question #111 : Basic Single Variable Algebra

Add and simplify the following rational expression:

$\frac{\sqrt{5}}{\sqrt{7}}+\frac{\sqrt{10}}{\sqrt{3}}$

Possible Answers:

$17\sqrt{\frac{5}{21}}$

$\sqrt{\frac{3}{2}}$

$\small \frac{\sqrt{35}}{7}+\frac{\sqrt{30}}{3}$

No real solution

$\frac{\sqrt{85}}{\sqrt{21}}$

Correct answer:

$\small \frac{\sqrt{35}}{7}+\frac{\sqrt{30}}{3}$

Explanation:

To add any fractions together, they must first have a common denominator. We can obtain a common denominator of $\sqrt{21}$ if we multiply the first fraction by $\frac{\sqrt{3}}{\sqrt{3}}$ and the second one by $\frac{\sqrt{7}}{\sqrt{7}}$ . We therefore obtain:

$\frac{\sqrt{5}}{\sqrt{7}}\times\frac{\sqrt{3}}{\sqrt{3}} + \frac{\sqrt{10}}{\sqrt{3}}\times\frac{\sqrt{7}}{\sqrt{7}}$

$\small \frac{\sqrt{15}}{\sqrt{21}}+\frac{\sqrt{70}}{\sqrt{21}}=\frac{\sqrt{15}+\sqrt{70}}{\sqrt{21}}$

From there, we need to take out the radical in the denominator by multiplying by $\small \frac{\sqrt{21}}{\sqrt{21}}$ , as follows:

$\small \small \frac{\sqrt{15}+\sqrt{70}}{\sqrt{21}}\times\frac{\sqrt{21}}{\sqrt{21}}=\frac{\sqrt{315}+\sqrt{1470}}{21}$

From here, we can simplify the radicals above by finding their prime factors:

$\small \sqrt{315}=\sqrt{3*3*5*7}=3\sqrt{35}$

and

$\small \sqrt{1470}=\sqrt{2*5*3*7*7}=7\sqrt{30}$ .

We are therefore left with $\small \frac{3\sqrt{35}+7\sqrt{30}}{21}$ , which can be separated and reduced to our final answer,

$\small \frac{\sqrt{35}}{7}+\frac{\sqrt{30}}{3}$

Report an Error

View Algebra 2 Tutors

Alejandro
Certified Tutor

Kennesaw State University, Bachelor of Science, Computer Software Engineering.

View Algebra 2 Tutors

Travis
Certified Tutor

Delaware State University, Bachelor of Science, Mathematics.

View Algebra 2 Tutors

Mayowa
Certified Tutor

Logan University, Bachelor of Science, Biology, General.

All Algebra II Resources

10 Diagnostic Tests 630 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

GMAT Tutors in Washington DC, Algebra Tutors in Chicago, ACT Tutors in Denver, Math Tutors in Miami, Spanish Tutors in Seattle, LSAT Tutors in Dallas Fort Worth, Calculus Tutors in Los Angeles, Statistics Tutors in Denver, ACT Tutors in Seattle, English Tutors in San Diego

Popular Courses & Classes

GMAT Courses & Classes in Boston, LSAT Courses & Classes in Washington DC, ACT Courses & Classes in Seattle, SAT Courses & Classes in Phoenix, SAT Courses & Classes in San Diego, SSAT Courses & Classes in Chicago, MCAT Courses & Classes in Miami, GMAT Courses & Classes in Denver, GMAT Courses & Classes in Los Angeles, SAT Courses & Classes in Seattle

Popular Test Prep

GMAT Test Prep in Atlanta, SAT Test Prep in Seattle, ISEE Test Prep in Houston, GMAT Test Prep in Los Angeles, LSAT Test Prep in New York City, ISEE Test Prep in Denver, SAT Test Prep in San Francisco-Bay Area, GRE Test Prep in Washington DC, GRE Test Prep in Denver, LSAT Test Prep in Washington DC

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Algebra II : Expressions

Study concepts, example questions & explanations for Algebra II

All Algebra II Resources

Example Questions

Example Question #61 : Expressions

Example Question #1 : How To Multiply Polynomials

Example Question #1 : How To Multiply Polynomials

Example Question #62 : Expressions

Example Question #1 : Operations With Polynomials

Example Question #66 : Expressions

Example Question #2 : Simplifying Expressions

Example Question #21 : Simplifying Expressions

Example Question #68 : Expressions

Example Question #111 : Basic Single Variable Algebra

All Algebra II Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: