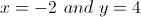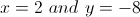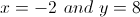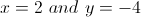We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

Algebra II : Equations

Study concepts, example questions & explanations for Algebra II

Create An Account

All Algebra II Resources

10 Diagnostic Tests 630 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #2321 : Algebra Ii

Simplify the expression by combining like terms.

Simplify:

5x^2+15x+18 = 6x^2-8x+9

Possible Answers:

x^2+23x+9 = 0

-x^2-23x+27 = 0

5x^2-23x-9 = 6x^2

11x^2-23x-9 = 0

x^2-23x-9 = 0

Correct answer:

x^2-23x-9 = 0

Explanation:

The original equation:

5x^2+15x+18 = 6x^2-8x+9

Now move all terms to one side, in this example, we will use the right side, but either side will work.

0 = 6x^2 - 8x + 9 -5x^2 -15x-18

As you can see, we subtracted the terms on the left from both sides, effectively moving them to the other side.

Regrouping the terms so that "like terms" are together. Like terms are defined by having the same power of x.

0= (6x^2-5x^2)+(-8x-15x)+(9-18)

Now, we add any terms that have like powers of x.

x^2-23x-9 = 0

Now that all terms have been combined, we are finished. The equation is simplified.

Report an Error

Example Question #131 : Systems Of Equations

Solve this system of equations.

7x+4y+9z=0

8x-3y-6z=12

2x-y-3z=5

Possible Answers:

x=-2 , y=-2 , z=2

x=-1 , y=2 , $z=-\frac{5}{3}$

$x=\frac{1}{2}$ , $y=\frac{3}{2}$ , z=-3

x=1 , y=2 , $z=-\frac{5}{3}$

x=5 , y=-9 , z=3

Correct answer:

x=1 , y=2 , $z=-\frac{5}{3}$

Explanation:

Equation 1: 7x+4y+9z=0

Equation 2: 8x-3y-6z=12

Equation 3: 2x-y-3z=5

Adding the terms of the first and second equations together will yield 15x+y+3z=12 .

Then, add that to the third equation so that the y and z terms are eliminated. You will get 17x=17 .

This tells us that x = 1. Plug this x = 1 back into the systems of equations.

7+4y+9z=0

8-3y-6z=12

2-y-3z=5

Now, we can do the rest of the problem by using the substitution method. We'll take the third equation and use it to solve for y.

2-y-3z=5

-y=3z+5-2

y=-3z-3

Plug this y-equation into the first equation (or second equation; it doesn't matter) to solve for z.

7+4y+9z=0

7+4(-3z-3) +9z=0

7-12z-12+9z=0

-5-3z=0

$z=-\frac{5}{3}$

We can use this z value to find y

y=-3z-3

$y=-3\left ( -\frac{5}{3}\right )-3$

y=2

So the solution set is x = 1, y = 2, and z = –5/3.

Report an Error

Example Question #2 : Solving Equations

Solve for : $x^{2}-144=0$

Possible Answers:

x=8,-4

x=12,-12

x=14,-14

x=10,-14

Correct answer:

x=12,-12

Explanation:

To solve this problem we can first add 144 to each side of the equation yielding $x^{2}=144$

Then we take the square root of both sides to get $\sqrt{x^{2}}=\sqrt{144}$

Then we calculate the square root of 144 which is $x=\pm12$ .

Report an Error

Example Question #1 : How To Subtract Trinomials

Solve this system of equations for :

2x + y = 12

x - 3y = 13

Possible Answers:

x = 9

x = 4

x = 7

x = 1

x = 11

Correct answer:

x = 7

Explanation:

Multiply the top equation by 3 on both sides, then add the second equation to eliminate the terms:

2x + y = 12

$3\cdot \left (2x + y \right )= 3\cdot 12$

6x+3y = 36

$\underline{x - 3y = 13}$

$7x\;\;\;\; \; =49$

$7x \div 7 =49 \div 7$

x = 7

Report an Error

Example Question #11 : Quadratic Equations

Solve for .

$y-7=\frac{4x+6y}{3}$

Possible Answers:

$y=-\frac{2}{3}x-7$

y=-{3}x-7

$y=\frac{4}{3}x-7$

$y=\frac{2}{3}x-7$

$y=-\frac{4}{3}x-7$

Correct answer:

$y=-\frac{4}{3}x-7$

Explanation:

$y-7=\frac{4x+6y}{3}$

Multiply both sides by 3:

$\frac{3}{1}(y-7)=(\frac{4x+6y}{3})\frac{3}{1}$

3(y-7)={4x+6y}

Distribute:

3y-21={4x+6y}

Subtract from both sides:

-21=4x+6y-3y

Add the terms together, and subtract from both sides:

-4x-21=3y

Divide both sides by :

$\frac{-4x-21=3y}{3}$

Simplify:

$y=-\frac{4}{3}x-7$

Report an Error

Example Question #134 : Systems Of Equations

Solve for :

x(x - 2) = x^2 -8

Possible Answers:

Correct answer:

Explanation:

Distribute the x through the parentheses:

x² –2x = x² – 8

Subtract x² from both sides:

–2x = –8

Divide both sides by –2:

x = 4

Report an Error

Example Question #3 : Solving Equations

Solve for :.

18x^3 - 8x = 0

Possible Answers:

$\left \{ - \frac{3}{2}, \frac{3}{2} \right\}$

$\left \{-\frac{2}{3}, \frac{2}{3} \right \}$

$\left \{-\frac{2}{3}, 0, \frac{2}{3} \right \}$

$\left \{ \frac{3}{2}, 0, -\frac{3}{2} \right\}$

Correct answer:

$\left \{-\frac{2}{3}, 0, \frac{2}{3} \right \}$

Explanation:

First factor the expression by pulling out :

18x^3 - 8x = 0

2x(9x^2-4) = 0

Factor the expression in parentheses by recognizing that it is a difference of squares:

2x(3x+2)(3x-2)= 0

Set each term equal to 0 and solve for the x values:

$2x=0 \rightarrow x=0$

$3x+2=0\rightarrow x=-\frac{2}{3}$

$3x-2=0\rightarrow x=\frac{2}{3}$

Report an Error

Example Question #1 : Solving Equations

Solve the system of equations.

4x+y=16

2x+3y=18

Possible Answers:

(-3,4)

(-4,3)

(4,3)

(3,4)

None of the other answers are correct.

Correct answer:

(3,4)

Explanation:

Isolate in the first equation.

y=16-4x

Plug into the second equation to solve for .

2x+3(16-4x)=18

2x+48-12x=18

-10x+48=30

-10x=-30

x=3

Plug into the first equation to solve for .

4(3)+y=16

12+y=16

y=4

Now we have both the and values and can express them as a point: (3,4) .

Report an Error

Example Question #2 : Solving Equations

Solve for and .

3x+2y=2

2x+2y=4

Possible Answers:

$x=-2\ and\ y=4$

$x=-2\ and\ y=8$

$x=2\ and\ y=-4$

$x=2\ and\ y=-8$

Cannot be determined.

Correct answer:

$x=-2\ and\ y=4$

Explanation:

1st equation: 3x+2y=2

2nd equation: 2x+2y=4

Subtract the 2nd equation from the 1st equation to eliminate the "2y" from both equations and get an answer for x:

Plug the value of into either equation and solve for :

2(-2)+2y=4

-4+2y=4

2y=4+4

2y=8

Report an Error

Example Question #3 : Solving Equations

What is a solution to this system of equations:

$\left\{\begin{matrix} x+2y-z=6\\ 2x+y+z=9\\ 3x+4y+z=18\end{matrix}\right.$

Possible Answers:

$\left\{\begin{matrix} x=3\\ y=2\\ z=1\end{matrix}\right.$

$\left\{\begin{matrix} x=3\\ y=-2\\ z=1\end{matrix}\right.$

$\left\{\begin{matrix} x=-3\\ y=2\\ z=1\end{matrix}\right.$

$\left\{\begin{matrix} x=-3\\ y=2\\ z=-1\end{matrix}\right.$

$\left\{\begin{matrix} x=3\\ y=-2\\ z=-1\end{matrix}\right.$

Correct answer:

$\left\{\begin{matrix} x=3\\ y=2\\ z=1\end{matrix}\right.$

Explanation:

Step 1: Multiply first equation by −2 and add the result to the second equation. The result is:

\left\{\begin{matrix} x+2y-z=6\\ -3y+3z=-3\\ 3x+4y+z=18\end{matrix}\right.

Step 2: Multiply first equation by −3 and add the result to the third equation. The result is:

\left\{\begin{matrix} x+2y-z=6\\ -3y+3z=-3\\ -2y+4z=0\end{matrix}\right.

Step 3: Multiply second equation by −23 and add the result to the third equation. The result is:

\left\{\begin{matrix} x+2y-z=6\\ -3y+3z=-3\\ 2z=2\end{matrix}\right.

Step 4: solve for z .

Step 5: solve for y .

-3y+3\times1=-3

Step 6: solve for x by substituting y=2 and z=1 into the first equation.

$x+2\times2-1=6$

x=3

Report an Error

View Algebra 2 Tutors

Bobby
Certified Tutor

University of Houston - Downtown, Bachelor of Science, Applied Mathematics.

View Algebra 2 Tutors

Reza
Certified Tutor

University of Sherbrooke, Doctor of Philosophy, Mathematics. University of Manitoba, Master of Science, Mathematics.

View Algebra 2 Tutors

Robert
Certified Tutor

Rensselaer Polytechnic Institute, Bachelors, Electrical Engineering. Brooklyn Polytechnic, Masters, Computer Science.

All Algebra II Resources

10 Diagnostic Tests 630 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Computer Science Tutors in Denver, Math Tutors in Miami, Physics Tutors in Houston, Reading Tutors in Miami, Spanish Tutors in San Diego, Reading Tutors in New York City, Physics Tutors in Boston, Biology Tutors in Philadelphia, Statistics Tutors in Houston, Chemistry Tutors in Los Angeles

Popular Courses & Classes

MCAT Courses & Classes in Dallas Fort Worth, Spanish Courses & Classes in San Diego, LSAT Courses & Classes in Washington DC, ISEE Courses & Classes in Washington DC, GRE Courses & Classes in Washington DC, MCAT Courses & Classes in Philadelphia, MCAT Courses & Classes in San Diego, ACT Courses & Classes in Phoenix, MCAT Courses & Classes in San Francisco-Bay Area, LSAT Courses & Classes in Miami

Popular Test Prep

LSAT Test Prep in Denver, ACT Test Prep in Houston, GMAT Test Prep in Boston, SSAT Test Prep in San Francisco-Bay Area, LSAT Test Prep in New York City, GMAT Test Prep in Miami, ACT Test Prep in Denver, ISEE Test Prep in New York City, SAT Test Prep in Phoenix, ACT Test Prep in Phoenix

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Algebra II : Equations

Study concepts, example questions & explanations for Algebra II

All Algebra II Resources

Example Questions

Example Question #2321 : Algebra Ii

Example Question #131 : Systems Of Equations

Example Question #2 : Solving Equations

Example Question #1 : How To Subtract Trinomials

Example Question #11 : Quadratic Equations

Example Question #134 : Systems Of Equations

Example Question #3 : Solving Equations

Example Question #1 : Solving Equations

Example Question #2 : Solving Equations

Example Question #3 : Solving Equations

All Algebra II Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: