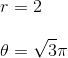All Algebra II Resources
Example Questions
Example Question #4781 : Algebra Ii
Write the complex number 


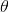
To see what the polar form of the number is, it helps to draw it on a graph, where the horizontal axis is the imaginary part and the vertical axis the real part. This is called the complex plane.

To find the angle 



Using trigonometric ratios, 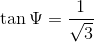

Then 
To find the distance 




Example Question #161 : Imaginary Numbers
Where does 
Cannot be determined
To the right of 0
At 0
To the left of 0
To the left of 0
Imaginary numbers do not fall on the number line by definition, since they are not real numbers. However, although i is an imaginary number equal to the square root of -1, 


Example Question #165 : Imaginary Numbers
Which complex number does this graph represent?

Real numbers are represented by the x-axis, and imaginary numbers are represented by the y-axis.
In complex numbers of the form 


Example Question #166 : Imaginary Numbers
Which complex number does this graph represent?

Real numbers are represented by the x-axis, and imaginary numbers are represented by the y-axis.
In complex numbers of the form 


Example Question #2 : Graphing Functions With Complex Numbers
Which of the following represents the real component of the complex number 
In complex numbers of the form 



Example Question #168 : Imaginary Numbers
Which of the following represents the imaginary component of the complex number -3 + ki, in which k is a constant?
In complex numbers of the form 




Example Question #169 : Imaginary Numbers
Which complex number does this graph represent?

Real numbers are represented by the x-axis, and imaginary numbers are represented by the y-axis.
In complex numbers of the form 


Example Question #170 : Imaginary Numbers
Which complex number does this graph represent?

Real numbers are represented by the x-axis, and imaginary numbers are represented by the y-axis.
In complex numbers of the form 


Example Question #1 : Absolute Value
Solve the following absolute value inequality:
To solve this inequality, it is best to break it up into two separate inequalities to eliminate the absolute value function:


Then, solve each one separately:
Combining these solutions gives:
Example Question #1 : Absolute Value Inequalities
Solve the inequality:


The inequality compares an absolute value function with a negative integer. Since the absolute value of any real number is greater than or equal to 0, it can never be less than a negative number. Therefore, 
Certified Tutor
Certified Tutor
All Algebra II Resources