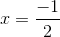Call Now to Set Up Tutoring:

(888) 888-0446

Algebra II : Algebra II

Study concepts, example questions & explanations for Algebra II

Create An Account

All Algebra II Resources

10 Diagnostic Tests 630 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #11 : Logarithms With Exponents

Use

$\log4=0.602$

and

$\log12=1.079$

Evaluate:

$\log64$

Possible Answers:

1.681

0.477

0.218

1.806

1.204

Correct answer:

1.806

Explanation:

Since the question gives,

$\log4=0.602$

and

$\log12=1.079$

To evaluate

$\log64$

manipulate the expression to use what is given.

$=\log4^3$

$=3\log4$

=3*0.602

=1.806

Report an Error

Example Question #380 : Mathematical Relationships And Basic Graphs

Simplify: $2e^{ln(2x+1)}$

Possible Answers:

4x+2

4x+1

$x+\frac{1}{2}$

$2^{2x+1}$

4x^2+4x+1

Correct answer:

4x+2

Explanation:

According to log rules, when an exponential is raised to the power of a logarithm, the exponential and log will cancel out, leaving only the power.

Simplify the given expression.

$2e^{ln(2x+1)} = 2(2x+1)$

Distribute the integer to both terms of the binomial.

The answer is: 4x+2

Report an Error

Example Question #11 : Logarithms With Exponents

Simplify: $5ln(e^{5(5-x)})$

Possible Answers:

125-25x

25-x

125-5x

x-5

5-x

Correct answer:

125-25x

Explanation:

The natural log has a default base of .

This means that the expression written can also be:

$5ln_e(e^{5(5-x)})$

Recall the log property that:

ln_k(k^n) = n

This would eliminate both the natural log and the base, leaving only the exponent.

The natural log and the base will be eliminated.

The expression will simplify to:

5[5(5-x)] = 5[25-5x] = 125-25x

The answer is: 125-25x

Report an Error

Example Question #11 : Logarithms With Exponents

Simplify: $2^{log_2(5x-6)}$

Possible Answers:

5x-4

10x-12

25x^2+60x-36

25x^2-60x-36

5x-6

Correct answer:

5x-6

Explanation:

The log property need to solve this problem is:

$b^{log_b x} = x$

The base and the log of the base are similar. They will both cancel and leave just the quantity of log based two.

$2^{log_2(5x-6)}=5x-6$

The answer is: 5x-6

Report an Error

Example Question #14 : Logarithms With Exponents

Solve: $log_{4}(8^3)$

Possible Answers:

$\frac{9}{2}$

$\frac{8}{3}$

Correct answer:

$\frac{9}{2}$

Explanation:

Rewrite the log so that the terms are in a fraction.

$log_{4}(8^3) = \frac{log(8^3)}{log( 4)}$

Both terms can now be rewritten in base two.

$\frac{log(8^3)}{log( 4)} = \frac{log((2^3)^3)}{log( 2^2)} = \frac{log(2)^9}{log(2)^2}$

The exponents can be moved to the front as coefficients.

$\frac{log(2)^9}{log(2)^2} = \frac{9log(2)}{2log(2)} = \frac{9}{2}$

The answer is: $\frac{9}{2}$

Report an Error

Example Question #381 : Mathematical Relationships And Basic Graphs

Which statement is true of $\frac{1}{5} \log _{5}N$ for all positive values of ?

Possible Answers:

$\frac{1}{5} \log _{5}N = \log_{5} (N - 1)$

$\frac{1}{5} \log _{5}N = \log_{5}\left ( \frac{1}{5} N \right )$

$\frac{1}{5} \log _{5}N = \log_{5} \sqrt[5]{N}$

$\frac{1}{5} \log _{5}N = \log_{5} (N - 5)$

$\frac{1}{5} \log _{5}N = N$

Correct answer:

$\frac{1}{5} \log _{5}N = \log_{5} \sqrt[5]{N}$

Explanation:

By the Logarithm of a Power Property, for all real , all N > 0 , $a > 0 , a \ne 1$

$b \log_{a} N = \log_{a}( N ^{b})$

Setting $b = \frac{1}{5} , a = 5$ , the above becomes

$\frac{1}{5} \log _{5}N = \log_{5} \left ( N^{\frac{1}{5}}\right )$

Since, for any a,b for which the expressions are defined,

$N^{\frac{1}{b}} = \sqrt[b]{N}$ ,

setting b = 5 , th equation becomes

$\frac{1}{5} \log _{5}N = \log_{5} \sqrt[5]{N}$ .

Report an Error

Example Question #15 : Logarithms With Exponents

Which statement is true of

$\log_{7} \sqrt[N]{7}$

for all integers N > 1 ?

Possible Answers:

$\log_{7} \sqrt[N]{7}= \frac{1}{N}$

$\log_{7} \sqrt[N]{7} = N - 1$

$\log_{7} \sqrt[N]{7}= \frac{7}{N}$

$\log_{7} \sqrt[N]{7} = -N$

$\log_{7} \sqrt[N]{7} = N - 7$

Correct answer:

$\log_{7} \sqrt[N]{7}= \frac{1}{N}$

Explanation:

Due to the following relationship:

$\sqrt[N]{7} = 7 ^{\frac{1}{N}}$ ; therefore, the expression

$\log_{7} \sqrt[N]{7}$

can be rewritten as

$\log_{7} \left ( 7 ^{\frac{1}{N}} \right )$

By definition,

$\log_{a} \left (a^{M} \right )= M$ .

Set a = 7 and $M = \frac{1}{N}$ , and the equation above can be rewritten as

$\log_{7} \left ( 7 ^{\frac{1}{N}} \right )= \frac{1}{N}$ ,

or, substituting back,

$\log_{7} \sqrt[N]{7}= \frac{1}{N}$

Report an Error

Example Question #1 : Solving Logarithms

Solve for :

$5^{x} = \left(\frac{1}{25}\right)^{4x-1}$

Possible Answers:

$x = \frac{2}{9}$

$x = \frac{1}{3}$

$x = \frac{1}{2}$

$x = \frac{-1}{2}$

$x = \frac{-2}{7}$

Correct answer:

$x = \frac{2}{9}$

Explanation:

To solve for , first convert both sides to the same base:

$5^{x} = \frac{1}{25}^{4x-1} = (5^{-2})^{4x-1} = 5^{-8x+2}$

Now, with the same base, the exponents can be set equal to each other:

x= - 8x +2

Solving for gives:

$x = \frac{2}{9}$

Report an Error

Example Question #2 : Solving Logarithms

Solve the equation:

$\log{_{4}}{x^{2}}+\log{_{4}}{3}=1$

Possible Answers:

$\frac{\sqrt{3}}{2}, -\frac{\sqrt{3}}{2}$

$\frac{\sqrt{6}}{3}, -\frac{\sqrt{6}}{3}$

$\frac{2\sqrt{3}}{3}, -\frac{2\sqrt{3}}{3}$

1,-1

$\frac{\sqrt{3}}{3}, -\frac{\sqrt{3}}{3}$

Correct answer:

$\frac{2\sqrt{3}}{3}, -\frac{2\sqrt{3}}{3}$

Explanation:

$\log{_{4}}{x^{2}}+\log{_{4}}{3}=1$

$\Rightarrow \log{_{4}}{x^{2}}+\log{_{4}}{3}=\log{_{4}}{4}$

$\Rightarrow log{_{4}}{(x^{2}\times 3)}=\log{_{4}}{4}$

$\Rightarrow 3x^{2}=4$

$\Rightarrow x^{2}=\frac{4}{3}$

$\Rightarrow x=\frac{2\sqrt{3}}{3}, x=-\frac{2\sqrt{3}}{3}$

Report an Error

Example Question #3 : Solving Logarithms

Use $\small \small \log_23\approx 1.5850$ to approximate the value of $\small \log_2 24$ .

Possible Answers:

$\small \log_2 24\approx 3.4150$

$\small \log_2 24\approx 12.5850$

$\small \log_2 24\approx 3.5850$

$\small \log_2 24\approx 4.5850$

$\small \log_2 24\approx 12.6800$

Correct answer:

$\small \log_2 24\approx 4.5850$

Explanation:

Rewrite as a product that includes the number :

$\small \log_2 24 = \log_2 (2^3 \cdot 3)$

Then we can split up the logarithm using the Product Property of Logarithms:

$\small \log_2 (2^3\cdot 3) = \log_2 2^3 + \log_2 3$

$\small =3+\log_2 3$

$\small \approx 3 + 1.5850$

Thus,

$\small \log_2 24 \approx 4.5850$ .

Report an Error

View Algebra 2 Tutors

Nicholas
Certified Tutor

Fordham University, Bachelors, Business Administration and Management. Boston University, Master of Arts, Multimedia.

View Algebra 2 Tutors

Joshua
Certified Tutor

Cornerstone University, Bachelor in Arts, Elementary School Teaching.

View Algebra 2 Tutors

Dylan
Certified Tutor

University of California-Berkeley, Bachelor of Science, Cognitive Science.

All Algebra II Resources

10 Diagnostic Tests 630 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Spanish Tutors in Washington DC, Spanish Tutors in Houston, Chemistry Tutors in New York City, English Tutors in Philadelphia, Calculus Tutors in Philadelphia, ISEE Tutors in New York City, LSAT Tutors in Philadelphia, SSAT Tutors in New York City, GMAT Tutors in Washington DC, MCAT Tutors in Dallas Fort Worth

Popular Courses & Classes

GRE Courses & Classes in Houston, SAT Courses & Classes in Washington DC, SSAT Courses & Classes in Chicago, SAT Courses & Classes in Houston, ISEE Courses & Classes in New York City, GRE Courses & Classes in San Diego, SSAT Courses & Classes in Los Angeles, ACT Courses & Classes in Boston, ISEE Courses & Classes in Phoenix, GRE Courses & Classes in Denver

Popular Test Prep

SAT Test Prep in Boston, GRE Test Prep in Houston, SSAT Test Prep in Houston, ACT Test Prep in Miami, ACT Test Prep in Atlanta, SSAT Test Prep in Atlanta, ISEE Test Prep in San Diego, SSAT Test Prep in Boston, SAT Test Prep in Houston, GMAT Test Prep in Atlanta

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Algebra II : Algebra II

Study concepts, example questions & explanations for Algebra II

All Algebra II Resources

Example Questions

Example Question #11 : Logarithms With Exponents

Example Question #380 : Mathematical Relationships And Basic Graphs

Example Question #11 : Logarithms With Exponents

Example Question #11 : Logarithms With Exponents

Example Question #14 : Logarithms With Exponents

Example Question #381 : Mathematical Relationships And Basic Graphs

Example Question #15 : Logarithms With Exponents

Example Question #1 : Solving Logarithms

Example Question #2 : Solving Logarithms

Example Question #3 : Solving Logarithms

All Algebra II Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: