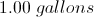Call Now to Set Up Tutoring:

(888) 888-0446

Algebra II : Algebra II

Study concepts, example questions & explanations for Algebra II

Create An Account

All Algebra II Resources

10 Diagnostic Tests 630 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #131 : Solving Rational Expressions

Solve for x

$\frac{12}{(x+4)}=\frac{9}{(5-x)}$

Possible Answers:

31.5

1.71

Correct answer:

1.71

Explanation:

The correct answer is 1.71 . Cross multiplying the equation in the question will give 12(5-x)=9(x+4) . This is simplified to 60-5x=9x+36 . Combining like terms gives 14x=24 . Finally, isolating gives 24/14 or 1.71 .

Report an Error

Example Question #1533 : High School Math

Sarah notices her map has a scale of $\frac{1}{4}\; in=1\; mile$ . She measures $12.5\; in$ between Beaver Falls and Chipmonk Cove. How far apart are the cities?

Possible Answers:

$75\; miles$

$50\; miles$

$90\; miles$

$60\; miles$

$25\; miles$

Correct answer:

$50\; miles$

Explanation:

$\frac{1}{4}\; in=1\; mile$ is the same as $1\; in = 4\; miles$

So to find out the distance between the cities

$12.5\; in \cdot \frac{4\; miles}{1\;in }=50\; miles$

Report an Error

Example Question #2 : Proportionalities

If an object is hung on a spring, the elongation of the spring varies directly as the mass of the object. A 20 kg object increases the length of a spring by exactly 7.2 cm. To the nearest tenth of a centimeter, by how much does a 32 kg object increase the length of the same spring?

Possible Answers:

$4.5 \textrm{ cm}$

$11.5 \textrm{ cm}$

$8.4 \textrm{ cm}$

$9.1\textrm{ cm}$

$18.4 \textrm{ cm}$

Correct answer:

$11.5 \textrm{ cm}$

Explanation:

Let M,L be the mass of the weight and the elongation of the spring. Then for some constant of variation ,

L = kM

We can find by setting M = 20,L=7.2 from the first situation:

$7.2 = k \cdot 20$

$k = 7.2 \div 20 = 0.36$

so L = 0.36 M

In the second situation, we set M = 32 and solve for :

$L = 0.36 \cdot32 =11.52$

which rounds to 11.5 centimeters.

Report an Error

Example Question #1 : Proportionalities

Sunshine paint is made by mixing three parts yellow paint and one part red paint. How many gallons of yellow paint should be mixed with two quarts of red paint?

(1 gallon = 4 quarts)

Possible Answers:

$1.75\; gallons$

$1.50\; gallons$

$0.75\; gallons$

$1.00\; gallons$

$0.50\; gallons$

Correct answer:

$1.50\; gallons$

Explanation:

First set up the proportion:

$\frac{3\; parts \; yellow}{1 \; part\; red}=\frac{x \; quarts \; yellow}{2 \; quarts \; red}$

x = $6 \; quarts\;yellow\; paint$

Then convert this to gallons:

$6 \; quarts\; \cdot \frac{1 \; gallon}{4\; quarts}= 1.50\; gallons$

Report an Error

Example Question #2 : Proportionalities

Sally currently has 192 books. Three months ago, she had 160 books. By what percentage did her book collection increase over the past three months?

Possible Answers:

$83.3\%$

$120\%$

$10\%$

$20\%$

$80\%$

Correct answer:

$20\%$

Explanation:

To find the percentage increase, divide the number of new books by the original amount of books:

192-160=32

She has 32 additional new books; she originally had 160.

$\frac{32}{160} = \frac{16}{80} = 0.20=20\%$

Report an Error

Example Question #3 : Proportionalities

Find for the proportion $\frac{x}{100}=\frac{1}{4}$ .

Possible Answers:

Correct answer:

Explanation:

To find x we need to find the direct proportion. In order to do this we need to cross multiply and divide.

$\frac{x}{100}=\frac{1}{4}$

From here we mulitply 100 and 1 together. This gets us 100 and now we divide 100 by 4 which results in

x=25

Report an Error

Example Question #4 : Proportionalities

On a map of the United States, Mark notices a scale of $\small in = 250$ miles . If the distance between New York City and Los Angeles in real life is 2400 miles , how far would the two cities be on Mark's map?

Possible Answers:

2.4

4.8

9.6

Correct answer:

9.6

Explanation:

If the real distance between the two cities is 2400 miles , and 250 miles = inch , then we can set up the proportional equation:

$\frac{1 in}{250 miles}=\frac{xin}{2400 miles}$

250x=2400

x = 9.6

Report an Error

Example Question #3 : Proportionalities

If $\small \small \small \frac{x}{108}=\frac{20}{y}$ and $\small \frac{224}{y}=\frac{14}{3}$ , find $\small x$ and $\small y$ .

Possible Answers:

$\small x=135, y=16$

$\small x=2, y=1045$

$\small x=45, y=48$

$\small x=6, y= 672$

$\small x=720, y=3$

Correct answer:

$\small x=45, y=48$

Explanation:

We cannot solve the first equation until we know at least one of the variables, so let's solve the second equation first to solve for $\small y$ . We therefore get:

$\small \frac{224}{y}=\frac{14}{3}\rightarrow14y=672\rightarrow y=48$

With our $\small y$ , we can now find x using the first equation:

$\small \frac{x}{108}=\frac{20}{48}\rightarrow48x=2160\rightarrow x=45$

We therefore get the correct answer of $\small x=45$ and $\small y=48$ .

Report an Error

Example Question #132 : Algebraic Functions

If an object is hung on a spring, the elongation of the spring varies directly with the mass of the object. A 33 kilogram object increases the length of a spring by exactly 6.6 centimeters. To the nearest tenth of a kilogram, how much mass must an object posess to increase the length of that same spring by exactly 10 centimeters?

Possible Answers:

$50 \textrm{ kg}$

$80 \textrm{ kg}$

$40 \textrm{ kg}$

$200 \textrm{ kg}$

$100 \textrm{ kg}$

Correct answer:

$50 \textrm{ kg}$

Explanation:

Let M,L be the mass of the weight and the elongation of the spring, respectively. Then for some constant of variation ,

L = kM .

We can find by setting M = 33,L=6.6 :

$6.6 = k \cdot 33$

$k = 6.6 \div 33 = 0.2$

Therefore L = 0.2 M .

Set L = 10 and solve for :

10= 0.2 M

$M = 10 \div 0.2 = 50$ kilograms

Report an Error

Example Question #5 : Proportionalities

If is directly proportional to and when a=24 at b=12 , what is the value of the constant of proportionality?

Possible Answers:

2.5

1.5

Correct answer:

Explanation:

The general formula for direct proportionality is

a=kb

where is the proportionality constant. To find the value of this , we plug in a=24 and b=12

24=12k

Solve for by dividing both sides by 12

$\frac{24}{12}=\frac{12k}{12}$

2=k

So k=2 .

Report an Error

View Algebra 2 Tutors

Bruce
Certified Tutor

University of Florida, Bachelor of Science, Mathematics. University of Florida, Master of Science, Mathematics.

View Algebra 2 Tutors

Thavisha
Certified Tutor

Minnesota State University-Mankato, Bachelor of Science, Mathematics.

View Algebra 2 Tutors

Samantha
Certified Tutor

Middlesex County College, Associate in Science, Sustainability Studies.

All Algebra II Resources

10 Diagnostic Tests 630 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Computer Science Tutors in Los Angeles, Biology Tutors in Denver, Computer Science Tutors in Phoenix, Reading Tutors in New York City, Physics Tutors in Miami, LSAT Tutors in Chicago, Statistics Tutors in Dallas Fort Worth, GMAT Tutors in Houston, LSAT Tutors in Atlanta, Chemistry Tutors in Boston

Popular Courses & Classes

GRE Courses & Classes in Boston, GMAT Courses & Classes in Denver, MCAT Courses & Classes in Philadelphia, MCAT Courses & Classes in Los Angeles, LSAT Courses & Classes in San Diego, ACT Courses & Classes in Houston, ACT Courses & Classes in Philadelphia, Spanish Courses & Classes in Washington DC, Spanish Courses & Classes in Philadelphia, GMAT Courses & Classes in Atlanta

Popular Test Prep

SAT Test Prep in Houston, LSAT Test Prep in Atlanta, SAT Test Prep in Miami, SAT Test Prep in Los Angeles, SSAT Test Prep in Miami, LSAT Test Prep in Los Angeles, SSAT Test Prep in Los Angeles, ACT Test Prep in Los Angeles, GMAT Test Prep in Denver, SSAT Test Prep in Houston

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Algebra II : Algebra II

Study concepts, example questions & explanations for Algebra II

All Algebra II Resources

Example Questions

Example Question #131 : Solving Rational Expressions

Example Question #1533 : High School Math

Example Question #2 : Proportionalities

Example Question #1 : Proportionalities

Example Question #2 : Proportionalities

Example Question #3 : Proportionalities

Example Question #4 : Proportionalities

Example Question #3 : Proportionalities

Example Question #132 : Algebraic Functions

Example Question #5 : Proportionalities

All Algebra II Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: