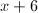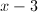Our first step in this problem would be to distribute the exponent on the second term, which makes the expression become:

We then multiply like terms, remembering that multiplying like terms with exponents means we will add the exponent, so the expression becomes:

a. Like when dividing fractions, change the division sign to multiplication and use the reciprocal of the divisor. 

b. Factor the trinomials in the numerator of both terms.

c. Cancel any common factors between the numerators and denominators.

This will leave: 

d. Multiply to simplify.

This problem will involve using the FOIL method to combine the first two parenthetical terms and then the distributive property to combine what is left. However, we can save time if we recognize that the first two parentheses are in form , with  and . We can therefore combine these two parentheses in form , and therefore:

Now we can use FOIL to find that:

which gives us a final answer of

To evaluate the expression, we will need to conduct the FOIL method on the first two polynomials and then use the distributive property to reach a final answer. Therefore:

which equals

Using the distributive property, we obtain:

which equals

To divide monomials, we subtract the exponents of the like terms. Therefore:

and 

Therefore:

In order to solve this equation, we must first simplify it so that we can cancel common factors between the numerator and the denominator.

In the above equation, we can first factor a  from . This gives us:

This is easier for us to factor. In order to factor this, we need to see which factors of  have a sum of . This turns out to be  and . Therefore, we can simplify this expression into:

Next, we need to simplify .

This is a difference of perfect squares. Therefore, its factors are .

Now we need to simplify .

This is a perfect square trinomial. Therefore, this simplifies in the form . Note that this is negative since in order for the middle term to be negative, the sign of  must be negative as well.

Finally, we have to simplify .

To factor this, we need to see what multiples of  (the first term, , multiplied by the third term, ) have a sum of positive . This turns out to be positive  plus a negative . Since our first term is , we need to determine which of our factors is a multiple of . We can see that this is only , which means that our factors will be positive  and negative . Therefore, when we simplify our expression, we get a result of

Now our expression looks like

The  in the numerator cancels with the  in the denominator, the  in the numerator cancels with the  in the denominator, and one of the  factors in the numerator cancels with the  in the denominator. This gives us our solution of:

Either using synthetic division by 2 or using x=2 in the remainder theorem are 2 short-cuts to performing the long division of this polynomial.

First, factor the numerator. We need factors that multiply to and add to .

We can plug the factored terms into the original expression.

Note that appears in both the numerator and the denominator. This allows us to cancel the terms.

This is our final answer.

The numerator is equivalent to

The denominator is equivalent to

Dividing the numerator by the denominator, one gets

It's much easier to use factoring and canceling than it is to use long division for this problem. 9x² – 1 is a difference of squares. The difference of squares formula is a² – b² = (a + b)(a – b). So 9x² – 1 = (3x + 1)(3x – 1). Putting the numerator and denominator together, (9x² – 1) / (3x – 1) = (3x + 1)(3x – 1) / (3x – 1) = 3x + 1.