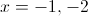Call Now to Set Up Tutoring:

(888) 888-0446

Algebra 1 : Variables

Study concepts, example questions & explanations for Algebra 1

Create An Account

All Algebra 1 Resources

10 Diagnostic Tests 557 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : How To Find The Solution Of A Rational Equation With A Binomial Denominator

Find the values of which will make the given rational expression undefined:

$\frac{x+5}{\left ( x-1 \right )\left ( x+2 \right )}$

Possible Answers:

x = -5, +2

x = -1, 2

x = -1, -2

x = 1, -2

x = -5, 1

Correct answer:

x = 1, -2

Explanation:

If $\left ( x-1 \right ) = 0$ or $\left ( x+2 \right ) =0$ , the denominator is 0, which makes the expression undefined.

This happens when x = 1 or when x = -2.

Therefore the correct answer is x = 1, -2 .

Report an Error

Example Question #3 : How To Find The Solution Of A Rational Equation With A Binomial Denominator

$\frac{y+1}{8y+2} + \frac{3}{y} = \frac{5}{3}$

Solve for .

Possible Answers:

y=-1 , y=4

$y=-\frac{5}{2}$

y=6 , $y=-\frac{7}{15}$

y=4 , y=0

y=2 , $y=-\frac{9}{37}$

Correct answer:

y=2 , $y=-\frac{9}{37}$

Explanation:

The two fractions on the left side of the equation need a common denominator. We can easily do find one by multiplying both the top and bottom of each fraction by the denominator of the other.

$\frac{y+1}{8y+2}\cdot \frac{y}{y}$ becomes $\frac{y^{2}+y}{(y)(8y+2)}$ .

$\frac{3}{y}\cdot \frac{8y+2}{8y+2}$ becomes $\frac{24y+6}{(y)(8y+2)}$ .

Now add the two fractions: $\frac{y^{2}+25y+6}{(y)(8y+2)}$

To solve, multiply both sides of the equation by (y)(8y+2) , yielding

$y^{2}+25y+6 = \frac{(40y^{2}+10y)}{3}$ .

Multiply both sides by 3:

$3y^{2}+75y+18 = 40y^{2}+ 10y$

Move all terms to the same side:

$37y^{2}-65y-18 = 0$

This looks like a complicated equation to factor, but luckily, the only factors of 37 are 37 and 1, so we are left with

(37y+9)(y-2) .

Our solutions are therefore

y=2

and

$y=-\frac{9}{37}$ .

Report an Error

Example Question #6 : How To Find The Solution Of A Rational Equation With A Binomial Denominator

Simplify the expression:

$\frac{x^{3}-5x^{2}+6x}{x-3}$

Possible Answers:

$\frac{x}{x-3}$

$x^{2}-2x$

$x^{2}-5x-3$

$x^{2}-3x$

x-2

Correct answer:

$x^{2}-2x$

Explanation:

First, factor out x from the numerator:

$\frac{x^{3}-5x^{2}+6x}{x-3}$ $=\frac{x(x^{2}-5x+6)}{x-3}$

Notice that the resultant expression in the parentheses is quadratic. This expression can be further factored:

$=\frac{x(x-2)(x-3)}{x-3}$

We can then cancel the (x-3) which appears in both the numerator and denominator:

$=\frac{x(x-2)}{1}$

Finally, distribute the x outside of the parentheses to reach our answer:

$=x^{2}-2x$

Report an Error

Example Question #1 : How To Find The Solution Of A Rational Equation With A Binomial Denominator

Solve for .

$2=\frac{10}{3y+2x^{2}}$

Possible Answers:

$y=\frac{3}{5}+\frac{3}{2}x^{2}$

$y=10+4x^{2}$

None of the other answers.

$y=\frac{4}{6}x^{2}-10$

Correct answer:

$y=\frac{3}{5}+\frac{3}{2}x^{2}$

Explanation:

Multiply each side by $3y+2x^{2}$

$2(3y+2x^{2})=10$

Distribute 2 to each term of the polynomial.

$6y+4x^{2}=10$

Divide the polynomial by 6.

$6(y+\frac{2}{3}x^{2})=10$

Divide each side by 6.

$y+\frac{2}{3}x^{2}=\frac{5}{3}$

Subtract the term from each side.

$y=\frac{5}{3}-\frac{2}{3}x^{2}$

Report an Error

Example Question #8 : How To Find The Solution Of A Rational Equation With A Binomial Denominator

Solve for .

$3=\frac{10}{k+2}$

Possible Answers:

$\frac{3}{4}$

$\frac{8}{3}$

$\frac{-4}{3}$

$\frac{4}{3}$

Correct answer:

$\frac{4}{3}$

Explanation:

Multiply each side by (k+2)

3(k+2)=10

Distribute 3 to the terms in parentheses.

3k+6=10

Subtract 6 from each side of the equation.

3k=4

Divide each side by 3.

$k=\frac{4}{3}$

Report an Error

Example Question #9 : How To Find The Solution Of A Rational Equation With A Binomial Denominator

Solve for .

$5=\frac{105}{n^{2}+5}$

Possible Answers:

$\sqrt{19}$

$\sqrt{80}$

Correct answer:

Explanation:

$5=\frac{105}{n^{2}+5}$

Multiply each side of the equation by $n^{2}+5$

$5(n^{2}+5)=105$

Distribute 5 to each term in parentheses.

$5n^{2}+25=105$

Subtract 25 from each side of equation.

$5n^{2}=80$

Divide each side of equation by 5.

$n^{2}=16$

Square root of each side of equation.

n=4

Report an Error

Example Question #4 : How To Find The Solution Of A Rational Equation With A Binomial Denominator

$\small \frac{x^2-5x-6}{x+1}$

For all values $x\neq -1$ , which of the following is equivalent to the expression above?

Possible Answers:

$\small x+6$

$\small x-3$

$\small x-6$

$\small x-2$

Correct answer:

$\small x-6$

Explanation:

First, factor the numerator. We need factors that multiply to $\small -6$ and add to $\small -5$ .

$\small 1*-6=-6\ \text{and}\ 1+(-6)=-5$

$\small x^2-5x-6=(x-6)(x+1)$

We can plug the factored terms into the original expression.

$\small \frac{x^2-5x-6}{x+1}=\frac{(x-6)(x+1)}{(x+1)}$

Note that $\small (x+1)$ appears in both the numerator and the denominator. This allows us to cancel the terms.

$\frac{(x-6)(x+1)}{(x+1)}=(x-6)$

This is our final answer.

Report an Error

Example Question #1 : How To Factor A Polynomial

Factor the following:

x^2-7x+6

Possible Answers:

x(x-6)

(x-6)(x-1)

(x-6)(x+1)

None of the available answers

(x-5)(x+2)

Correct answer:

(x-6)(x-1)

Explanation:

We will discuss coefficients in the general equation:

ax^2 +bx+c

In this case, is positive and is negative, and a=1 , so we know our answer involves two negative numbers that are factors of and add to . The answer is:

(x-6)(x-1)

Report an Error

Example Question #4 : Solving By Factoring

Solve for : $x^{2}+16x=-28$

Possible Answers:

x=1,28

x=-4,-7

x=2,14

x=-2,-14

Correct answer:

x=-2,-14

Explanation:

This is a factoring problem so we need to get all of the variables on one side and set the equation equal to zero. To do this we subtract from both sides to get $x^{2}+16x+28=0$

Think of the equation in this format to help with the following explanation. $ax^{2}+bx+c=0$

We must then factor to find the solutions for . To do this we must make a factor tree of which is 28 in this case to find the possible solutions. The possible numbers are $1\cdot 28$ , $2\cdot 14$ , $4\cdot 7$ .

Since is positive we know that our factoring will produce two positive numbers.

We then use addition with the factoring tree to find the numbers that add together to equal . So 28+1=29 , 2+14=16 , and 4+7=11

Success! 14 plus 2 equals . We then plug our numbers into the factored form of (x+2)(x+14)=0

We know that anything multiplied by 0 is equal to 0 so we plug in the numbers for which make each equation equal to 0 so in this case x=-2,-14 .

Report an Error

Example Question #1 : How To Factor A Polynomial

Solve by factoring:

$x^{2} + 2x - 15$

Possible Answers:

x = -3, 5

x = 15

x = 5, -5

x= 3, -3

x = 3, -5

Correct answer:

x = 3, -5

Explanation:

By factoring one gets

$y = (x-3)\left ( x + 5 \right )$

Now setting each of the two factors to 0 (using the zero property), one gets

x= 3 or x= -5

Report an Error

View Algebra Tutors

Ezam
Certified Tutor

University of the West Indies, Bachelor of Science, Mathematics and Computer Science. University of Phoenix-Central Valley Ca...

View Algebra Tutors

Magdy
Certified Tutor

Cairo University, Egypt, Bachelor of Science, Electrical Engineering. New Mexico State University-Main Campus, Doctor of Phil...

View Algebra Tutors

Noah
Certified Tutor

Vanderbilt University, Bachelor of Science, Biochemistry.

All Algebra 1 Resources

10 Diagnostic Tests 557 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

SSAT Tutors in Philadelphia, Calculus Tutors in Boston, Algebra Tutors in Los Angeles, LSAT Tutors in Houston, GRE Tutors in San Diego, Reading Tutors in Washington DC, Algebra Tutors in Chicago, Biology Tutors in San Francisco-Bay Area, Reading Tutors in Los Angeles, Statistics Tutors in Los Angeles

Popular Courses & Classes

GMAT Courses & Classes in Houston, ISEE Courses & Classes in Boston, Spanish Courses & Classes in San Francisco-Bay Area, GMAT Courses & Classes in Denver, GRE Courses & Classes in Seattle, MCAT Courses & Classes in Washington DC, Spanish Courses & Classes in Chicago, SAT Courses & Classes in Philadelphia, MCAT Courses & Classes in San Francisco-Bay Area, ACT Courses & Classes in Chicago

Popular Test Prep

ACT Test Prep in Chicago, GRE Test Prep in Atlanta, GMAT Test Prep in Los Angeles, GMAT Test Prep in Houston, SAT Test Prep in Atlanta, GRE Test Prep in San Diego, ISEE Test Prep in Boston, SAT Test Prep in Chicago, SSAT Test Prep in Washington DC, SSAT Test Prep in Seattle

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Algebra 1 : Variables

Study concepts, example questions & explanations for Algebra 1

All Algebra 1 Resources

Example Questions

Example Question #1 : How To Find The Solution Of A Rational Equation With A Binomial Denominator

Example Question #3 : How To Find The Solution Of A Rational Equation With A Binomial Denominator

Example Question #6 : How To Find The Solution Of A Rational Equation With A Binomial Denominator

Example Question #1 : How To Find The Solution Of A Rational Equation With A Binomial Denominator

Example Question #8 : How To Find The Solution Of A Rational Equation With A Binomial Denominator

Example Question #9 : How To Find The Solution Of A Rational Equation With A Binomial Denominator

Example Question #4 : How To Find The Solution Of A Rational Equation With A Binomial Denominator

Example Question #1 : How To Factor A Polynomial

Example Question #4 : Solving By Factoring

Example Question #1 : How To Factor A Polynomial

All Algebra 1 Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: