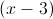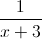Call Now to Set Up Tutoring:

(888) 888-0446

Algebra 1 : Variables

Study concepts, example questions & explanations for Algebra 1

Create An Account

All Algebra 1 Resources

10 Diagnostic Tests 557 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : How To Find The Solution To A Binomial Problem

Solve for in terms of :

$\frac{4}{3}x-3=\frac{2}{9}y$

Possible Answers:

$x=\frac{8}{27}y-3$

$x=\frac{-8}{27}y+3$

$x=\frac{1}{6}y-\frac{9}{4}$

$x=\frac{1}{6}y+\frac{9}{4}$

$x=\frac{8}{27}y+3$

Correct answer:

$x=\frac{1}{6}y+\frac{9}{4}$

Explanation:

First, isolate X onto one side of the equation:

$\frac{4}{3}X-3=\frac{2}{9}Y$

$\frac{4}{3}X=\frac{2}{9}Y+3$

Next, divide both sides of the equation by 4/3:

$\frac{4}{3}\div \frac{4}{3}X=\frac{4}{3}\div \frac{2}{9}Y+\frac{4}{3}\div \frac{3}{1}$

$\frac{3}{4}\cdot \frac{4}{3}X=\frac{3}{4}\cdot \frac{2}{9}Y+\frac{3}{4}\cdot \frac{3}{1}$

$X=\frac{6}{36}Y+\frac{9}{4}$

When simplified, your answer should be:

$X=\frac{1}{6}Y+\frac{9}{4}$

Report an Error

Example Question #1 : How To Find The Solution To A Binomial Problem

Solve for

-1 = 6 + x

Possible Answers:

Correct answer:

Explanation:

-1 = 6 + x

-1-6 = 6+x-6

-7 = x

Report an Error

Example Question #3 : How To Find The Solution To A Binomial Problem

Solve for

3 = -6 + x

Possible Answers:

Correct answer:

Explanation:

$\\3 = -6 + x \\3 + 6 = -6 + x + 6 \\9 = x$

Report an Error

Example Question #3 : How To Find The Solution To A Binomial Problem

Solve for

3 = 2 - x

Possible Answers:

None of the other answers.

Correct answer:

Explanation:

$\\3 = 2 - x \\3 - 2 = 2 - x - 2\\ 1 = -x(-1) = x$

Report an Error

Example Question #1 : How To Find The Solution To A Binomial Problem

Solve for

19 = 7 + x

Possible Answers:

Correct answer:

Explanation:

$\\19 = 7 + x \\ 19 - 7 = 7 + x -7 \\ 12 = x$

Report an Error

Example Question #301 : Variables

Solve for

-9 = 82 + x

Possible Answers:

None of the other answers.

Correct answer:

Explanation:

$\\-9 = 82 + x \\ -9 - 82 = 82 + x - 82 \\-91 = x$

Report an Error

Example Question #302 : Variables

Solve for

1 = -3 + x

Possible Answers:

None of the other answers.

Correct answer:

Explanation:

$\\1 = -3 + x \\1 + 3 = -3 + x + 3\\ 4 = x$

Report an Error

Example Question #4 : Solving Rational Expressions

Simplify:

$\frac{2x-3}{3-2x}$

Possible Answers:

$\frac{3}{2}$

$\frac{2}{3}$

Correct answer:

Explanation:

Factor out from the numerator which gives us

$\left -(3-2x \right )$

Hence we get the following

$\frac{\left -(3-2x \right )}{3-2x}$

which is equal to

Report an Error

Example Question #1 : Factoring Rational Expressions

Simplify:

$\frac{x+3}{x^{2}+6x+9}$

Possible Answers:

$\frac{1}{\left ( x+3 \right )^{2}}$

$\frac{1}{x+3}$

$\left ( x-3 \right )$

$\left ( x+3 \right )^{2}$

$\left ( x+3 \right )$

Correct answer:

$\frac{1}{x+3}$

Explanation:

If we factors the denominator we get

$\left ( x+3 \right )^{2}$

Hence the rational expression becomes equal to

$\frac{\left ( x+3 \right )}{\left ( x+3 \right )^{2}}$

which is equal to $\frac{1}{\left ( x+3 \right )}$

Report an Error

Example Question #1 : How To Find The Solution Of A Rational Equation With A Binomial Denominator

Which of the following fractions is NOT equivalent to $- \frac{x-5}{2x + 3}$ ?

Possible Answers:

$\frac{x-5}{-2x-3}$

$\frac{x+5}{2x + 3}$

$\frac{x-5}{\left -(2x+3 \right )}$

$\frac{\left -(x-5 \right )}{2x+3}$

$\frac{-x+5}{2x+3}$

Correct answer:

$\frac{x+5}{2x + 3}$

Explanation:

We know that $-\frac{a}{b}$ is equivalent to $\frac{-a}{b}$ or $\frac{a}{-b}$ .

By this property, there is no way to get $\frac{x+5}{2x+3}$ from $-\frac{x-5}{2x+3}$ .

Therefore the correct answer is $\frac{x+5}{2x+3}$ .

Report an Error

View Algebra Tutors

Arnav
Certified Tutor

Rutgers University-Newark, Bachelor of Science, Biomedical Engineering.

View Algebra Tutors

Bagher
Certified Tutor

San Jose State University, Master's/Graduate, Physics.

View Algebra Tutors

Jeremy
Certified Tutor

University of Illinois at Chicago, Bachelor of Science, Physics.

All Algebra 1 Resources

10 Diagnostic Tests 557 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Math Tutors in Miami, Calculus Tutors in Houston, GRE Tutors in San Diego, Computer Science Tutors in Seattle, MCAT Tutors in Seattle, GMAT Tutors in Philadelphia, MCAT Tutors in Chicago, Algebra Tutors in Houston, ISEE Tutors in Dallas Fort Worth, ISEE Tutors in Chicago

Popular Courses & Classes

ISEE Courses & Classes in Philadelphia, GRE Courses & Classes in San Francisco-Bay Area, LSAT Courses & Classes in Boston, GMAT Courses & Classes in San Diego, MCAT Courses & Classes in Philadelphia, GMAT Courses & Classes in Philadelphia, LSAT Courses & Classes in Houston, SAT Courses & Classes in San Francisco-Bay Area, LSAT Courses & Classes in Miami, SAT Courses & Classes in Dallas Fort Worth

Popular Test Prep

GRE Test Prep in Denver, MCAT Test Prep in Denver, ACT Test Prep in Houston, GRE Test Prep in New York City, MCAT Test Prep in Dallas Fort Worth, SAT Test Prep in Denver, GMAT Test Prep in Houston, GRE Test Prep in Chicago, MCAT Test Prep in San Diego, MCAT Test Prep in Miami

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Algebra 1 : Variables

Study concepts, example questions & explanations for Algebra 1

All Algebra 1 Resources

Example Questions

Example Question #1 : How To Find The Solution To A Binomial Problem

Example Question #1 : How To Find The Solution To A Binomial Problem

Example Question #3 : How To Find The Solution To A Binomial Problem

Example Question #3 : How To Find The Solution To A Binomial Problem

Example Question #1 : How To Find The Solution To A Binomial Problem

Example Question #301 : Variables

Example Question #302 : Variables

Example Question #4 : Solving Rational Expressions

Example Question #1 : Factoring Rational Expressions

Example Question #1 : How To Find The Solution Of A Rational Equation With A Binomial Denominator

All Algebra 1 Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: