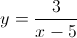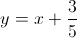1) Get  by itself. The first step, then, is to use order of operations backwards to decide where to start.

Take PEMDAS and flip it around. So subtraction/addition comes first, and therefore the 20 has to be the first to go.

2) Move the 20 to the other side of the equation using inverse operations. 20 is added to the  in the problem, so it needs to be subtracted from both sides.

3) Divide by  to get the  alone.

1) The first step in solving an equation is always to simplify as much as possible. Is there a factor that all terms have in common? They all have a negative sign, so can be factored out. It is not necessary to remove the ; however, the problem will be much simpler to solve without the negative signs to add confusion.

So divide both sides by :

2) Next, get  by itself using inverse order of operations. So subtract 13 from both sides and combine like terms:

Then divide both sides by five:

1) First, define your variables:

number of hours the truck is in use

total price

Even though the question gives the definitions, it's always helpful to rewrite them.

2) A flat price is the part of the price that is dependent on nothing. So the flat price stands alone:

3) The amount of money that the $20 rate will demand from the renter is dependent on the number of hours the truck is in use, as it is a rate and therefore involves some sort of time. Thus it is clear from looking at the definition of our variables that the 20 must be multiplied by  to determine how much more the renter must pay for the truck's use, on top of the $175. The two numbers must be added together to find the final price, which includes both.

First, use the distributive property to simplify the right side of the equation: 

.

Next, subtract  and add  to both sides to get 

.

Finally, divide both sides by  to get 

Use the distributive property to get . Isolate for  and you get 12. 

Subtract 3 from both sides of the equation.

Take the reciprocal of both sides of the equation

Multiply both sides by 4

Add 33 to both sides of equation

Take the square root of both sides of equation

A yard stick has 36 inches.  Let  length of piece one.  

Then, let  length of piece two.

The length of both pieces has to be 36 inches.

So,

After combining like terms we get:

Subtracting 6 from both sides gives:

Dividing both sides by 3 gives:, the length of piece one.

The length of piece two is given by  

Substituting in  gives:

Therefore, the lengths of the two pieces are 10 and 26 inches.

First, subtract 7 to both sides.

Factor the y on the left hand side.

Divide both sides by 3 – x.

Take an extra step by factoring the minus sign on the denominator.

Cancel the minus signs.

Add 9 to each side of the equation.

Multiply each side of the equation by 4.