Call Now to Set Up Tutoring:

(888) 888-0446

Algebra 1 : Algebra 1

Study concepts, example questions & explanations for Algebra 1

Create An Account

All Algebra 1 Resources

10 Diagnostic Tests 557 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

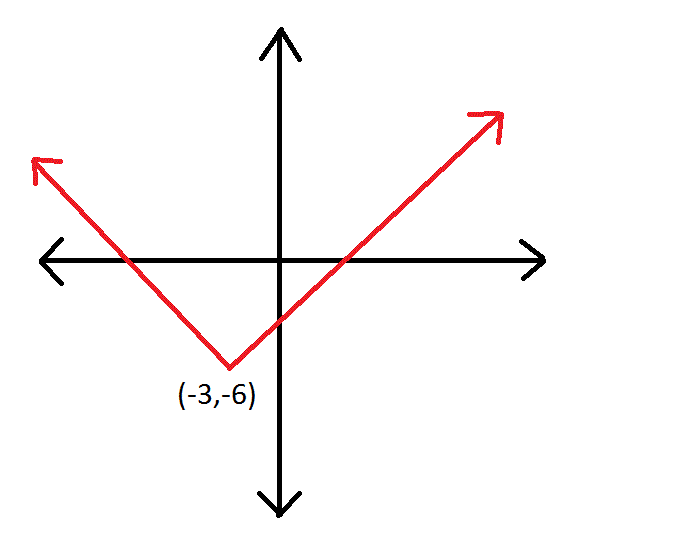
Example Question #2 : How To Graph An Absolute Value Function

Absolute_value

Which of these would most likely be the equation corresponding to the above graph?

Possible Answers:

y = | x + 6 | - 3

y = | x - 6 | - 3

y = | x + 3 | - 6

y = | x - 6 | + 3

y = | x - 3 | - 6

Correct answer:

y = | x + 3 | - 6

Explanation:

This is an absolute value graph. Its equation takes the form y = |x-h|+k , in which h,k represent the number of units that the base graph y = |x| is translated right and up respectively.

Since the graph of y = |x| is translated three units left and six units down, h = -3 and k = -6 .

Plug these values into the general form of the equation:

y = |x-(-3)|+(-6)

Simplify:

y = |x+3|-6

Report an Error

Example Question #43 : Functions And Lines

$\textup{What is the slope of } y=-4\left | x-2\right | \textup{ when } x=1?$

Possible Answers:

$\textup{It does not exist.}$

Correct answer:

Explanation:

$\textup{When }x=1\textup{ the expression inside the absolute value is negative,} \\\textup{so the function can be written as } y=-4(2-x)=4x-8,\textup{ with a slope of 4.}\\\textup{Plus, the slope changes to -4 when } x>2. \textup{ When } x=2 \textup{ it does not exist.}$

Report an Error

Example Question #2 : How To Graph An Absolute Value Function

$\textup{Find the lowest attainable value of }y \textup{ in } y=-4+ \left |4x^2-25 \right |.$

Possible Answers:

-2.5

2.5

Correct answer:

Explanation:

$\\ \left | 4x^2-25\right | \textup{cannot get any lower than zero,}\\\textup{so\textit{ y} cannot get any lower than} -4.$

Report an Error

Example Question #3331 : Algebra 1

$\textup{Which is an \textit{x}-intercept of the function } y=\left | -x^2-8x-16\right |-4.$

Possible Answers:

$\textup{None of the above.}$

Correct answer:

Explanation:

$\\ \textup{The function can be simplified as } \\y=\left | -(x+4)^2\right |-4=\left |(x+4)^2\right |-4=(x+4)^2-4.\\\textup{In order to find the \textit{x}-intercecpt, we solve the equation}\\0=(x+4)^2-4 \textup{ which becomes }\\(x+4)=\pm2\textup{ and has solution } -2 \textup{ and } -6.$

Report an Error

Example Question #1 : How To Find F(X)

A function is given by $f(x)=3x^{2}+3x-4$ . Find f(2) .

Possible Answers:

Correct answer:

Explanation:

Plugging in 2 wherever is present in the formula yields an answer of 14.

Report an Error

Example Question #1 : How To Find F(X)

If $f(x) = 0.3x^{2}-9x$ , evaluate f(10) .

Possible Answers:

Correct answer:

Explanation:

To solve this function, we simply need to understand that finding f(10) means that x=10 in this specific case. So, we can just substitute 10 in for .

$0.3(10)^{2}=0.3\cdot 100=30$

is equal to , so our final answer is

30-90 or .

Report an Error

Example Question #1 : Algebraic Functions

In which of these relations is not a function of ?

Possible Answers:

$y = \left | x-100\right |$

$x^{3}y = -1$

x+y = 1,000,000

$x = y^{2} + 1$

xy = 20

Correct answer:

$x = y^{2} + 1$

Explanation:

In the relation $x = y^{2} + 1$ , there are many values of that can be paired with more than one value of - for example, (2,1),(2,-1) .

To demonstrate that is a function of in the other examples, we solve each for :

x+y = 1,000,000 can be rewritten as y = 1,000,000 -x .

$x^{3}y = -1$ can be rewritten as $y = -\frac{1}{x^{3}}$

xy = 20 can be rewritten as $y = \frac{20}{x}$

$y = \left | x-100\right |$ need not be rewritten.

In each case, we see that for any value of , can be uniquely defined.

Report an Error

Example Question #3 : How To Find F(X)

f(x)= 2x^2 +x+2

$Evaluate\; f(6)$

Possible Answers:

Correct answer:

Explanation:

Report an Error

Example Question #1 : How To Find F(X)

What is the next number in the following sequence?

10, 20, 25, 50, 55, 110, 115,...

Possible Answers:

120

230

345

130

155

Correct answer:

230

Explanation:

To form this sequence, alternately multiply by 2 and add 5:

$\begin{matrix} 10 \cdot 2 = 20\\ 20+5 = 25\\ 25 \cdot 2 = 50\\ 50 + 5 = 55\\ 55 \cdot 2 = 110 \\ 110 + 5 = 115 \end{matrix}$

To keep the pattern going, double the seventh term to get the eighth:

$115 \cdot 2 = 230$

Report an Error

Example Question #2 : How To Find F(X)

Define $f (x) = 3 - \sqrt{x-1}$ and $g\left ( x\right ) = 3 + \sqrt{x-1}$

Evaluate $\left (fg \right ) (13)$

Possible Answers:

$\left (fg \right ) (13)$ is undefined.

Correct answer:

Explanation:

$f (x) = 3 - \sqrt{x-1}$

$f (13) = 3 - \sqrt{13-1} = 3 - \sqrt{12}$

$g(x) = 3 + \sqrt{x-1}$

$g(13) = 3 + \sqrt{13-1} = 3 + \sqrt{12}$

The easiest way to find $\left (fg \right ) (13)$ is to take advantage of the fact that the radical expressons are conjugates, and that their product follows the difference of squares pattern.

$fg (13) = f (13) \cdot g (13) = (3 - \sqrt{12}) (3 + \sqrt{12})= 3^{2} - \left (\sqrt{12} \right )^{2} = 9- 12 = -3$

Report an Error

View Algebra Tutors

Mudassara
Certified Tutor

CUNY College of Staten Island, Master of Arts, Business Administration and Management.

View Algebra Tutors

Dossevi
Certified Tutor

cole Ste Genevive Versailles, Bachelor of Science, Mathematics. Institut National Polytechnique de Grenoble, Master of Scienc...

View Algebra Tutors

Jeanene
Certified Tutor

Troy University, Bachelor of Science, Science Teacher Education.

All Algebra 1 Resources

10 Diagnostic Tests 557 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

ISEE Tutors in Miami, Statistics Tutors in New York City, Computer Science Tutors in Miami, Biology Tutors in Houston, Reading Tutors in Boston, GMAT Tutors in Dallas Fort Worth, Spanish Tutors in Houston, French Tutors in Boston, Calculus Tutors in Los Angeles, English Tutors in Los Angeles

Popular Courses & Classes

GRE Courses & Classes in Phoenix, SAT Courses & Classes in San Diego, SAT Courses & Classes in Denver, GMAT Courses & Classes in Seattle, ACT Courses & Classes in Phoenix, SSAT Courses & Classes in Washington DC, ISEE Courses & Classes in Philadelphia, SSAT Courses & Classes in New York City, SAT Courses & Classes in Washington DC, GRE Courses & Classes in Washington DC

Popular Test Prep

SSAT Test Prep in Houston, MCAT Test Prep in Atlanta, SAT Test Prep in Atlanta, SSAT Test Prep in Seattle, MCAT Test Prep in Los Angeles, GRE Test Prep in San Diego, ACT Test Prep in Phoenix, ISEE Test Prep in New York City, GMAT Test Prep in Los Angeles, GMAT Test Prep in Phoenix

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Algebra 1 : Algebra 1

Study concepts, example questions & explanations for Algebra 1

All Algebra 1 Resources

Example Questions

Example Question #2 : How To Graph An Absolute Value Function

Example Question #43 : Functions And Lines

Example Question #2 : How To Graph An Absolute Value Function

Example Question #3331 : Algebra 1

Example Question #1 : How To Find F(X)

Example Question #1 : How To Find F(X)

Example Question #1 : Algebraic Functions

Example Question #3 : How To Find F(X)

Example Question #1 : How To Find F(X)

Example Question #2 : How To Find F(X)

All Algebra 1 Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: