All Algebra 1 Resources
Example Questions
Example Question #7 : How To Graph A Line
Which equation matches the graph of the line shown?

An equation of a line is made of two parts: a slope and a y-intercept.
The y-intercept is where the function crosses the y-axis which in this problem it is 0.
The slope is determined by the rise of the function over the run which is 
Therefore your equation is:

Example Question #1 : How To Graph A Point
Which image depicts the point 





The first number, 
Example Question #1 : How To Graph A Point
The length of line segment 

To answer this question, we will have to manipulate the distance formula:
To get rid of the square root, we can square both sides:
and plug in the information given in the question.
At this point we can simply plug in the possible values to determine which combination of coordinates will make the equation above true.
Thus the correct coordinate is,

Example Question #1 : How To Graph A Point

Graph the following 4 points. They will be displayed as (x,y) pairs.
(A)
(B)
(C)
(D)





To graph these points we just need to remember that the first number is the x value and the second number is the y value. For (A) we have (1,3). So we move one tick over on the positive x-axis. Then from there we move up to the third tick on the y axis:

If the value is negative we must move in the other direction. So, for all 4 points,

Example Question #4 : How To Graph A Point
What are the coordinates of the point on the given graph?

When trying to determine coordinates of a point you need to look at the value of x first (how many units left or right the point is, then the y-value (how many up or down it is).
When you look at this point you see that it is moved right 2 units and up 1.
So your coordinates are:
Example Question #1 : Introduction To Functions
Which graph depicts a function?
Example Question #1 : Introduction To Functions
The graph below is the graph of a piece-wise function in some interval. Identify, in interval notation, the decreasing interval.
As is clear from the graph, in the interval between 









Example Question #581 : Functions And Graphs
Which equation best represents the following graph?
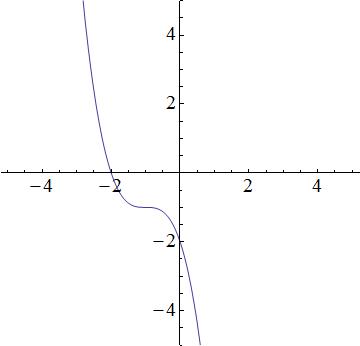
None of these
We have the following answer choices.
The first equation is a cubic function, which produces a function similar to the graph. The second equation is quadratic and thus, a parabola. The graph does not look like a prabola, so the 2nd equation will be incorrect. The third equation describes a line, but the graph is not linear; the third equation is incorrect. The fourth equation is incorrect because it is an exponential, and the graph is not an exponential. So that leaves the first equation as the best possible choice.
Example Question #333 : Sat Subject Test In Math I
What is the horizontal asymptote of the graph of the equation 
The asymptote of this equation can be found by observing that 



So the value that 


Example Question #3 : Solving Exponential Functions
What is/are the asymptote(s) of the graph of the function


An exponential equation of the form 



All Algebra 1 Resources
































![\left ( -\infty ,-2\right )\cup \left ( 1,3\right]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/60108/gif.latex)
![(-\infty ,-2]\cup (-\infty ,1)\cup (1,3)](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/60109/gif.latex)
![\left ( -\infty ,-2\right ]\cup \left ( 1,3 \right )](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/60107/gif.latex)























