All ACT Math Resources
Example Questions
Example Question #52 : How To Find The Length Of The Hypotenuse Of A Right Triangle : Pythagorean Theorem
Each of the following answer choices lists the side lengths of a different triangle. Which of these triangles does not have a right angle?


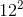

Example Question #1 : How To Find The Length Of The Side Of A Right Triangle
Given a right triangle with a leg length of 6 and a hypotenuse length of 10, find the length of the other leg, x.

64
16
8
4
8
Using Pythagorean Theorem, we can solve for the length of leg x:
x2 + 62 = 102
Now we solve for x:
x2 + 36 = 100
x2 = 100 – 36
x2 = 64
x = 8
Also note that this is proportionally a 3/4/5 right triangle, which is very common. Always look out for a side-to-hypoteneuse ratio of 3/5 or 4/5, or a side-to-side ratio of 3/4, in any right triangle, so that you may solve such triangles rapidly.
Example Question #1 : How To Find The Length Of The Side Of A Right Triangle
In a right triangle a hypotenuse has a length of 8 and leg has a length of 7. What is the length of the third side to the nearest tenth?
Using the pythagorean theorem, 82=72+x2. Solving for x yields the square root of 15, which is 3.9
Example Question #141 : Geometry
Given a right triangle with a leg length of 2 and a hypotenuse length of √8, find the length of the other leg, x.

10
6
2
√8
4
2
Using Pythagorean Theorem, we can solve for the length of leg x:
x2 + 22 = (√8)2 = 8
Now we solve for x:
x2 + 4 = 8
x2 = 8 – 4
x2 = 4
x = 2
Example Question #2 : How To Find The Length Of The Side Of A Right Triangle
The legs of a right triangle are 

Use the Pythagorean Theorem. The sum of both legs squared equals the hypotenuse squared.
Example Question #111 : Triangles
Find the length of segment 
The length of segment 
Note that triangles 






which simplifies to 
Example Question #1 : How To Find The Length Of The Side Of A Right Triangle
A handicap ramp is 

In this case, we are already given the length of the hypotenuse of the right triangle, but the Pythagorean formula still helps us. Plug and play, remembering that 



Thus, the ramp covers 
Example Question #141 : Geometry
You have two right triangles that are similar. The base of the first is 6 and the height is 9. If the base of the second triangle is 20, what is the height of the second triangle?
23
25
33
35
30
30
Similar triangles are proportional.
Base1 / Height1 = Base2 / Height2
6 / 9 = 20 / Height2
Cross multiply and solve for Height2
6 / 9 = 20 / Height2
6 * Height2= 20 * 9
Height2= 30
Example Question #1 : Right Triangles
A right triangle is defined by the points (1, 1), (1, 5), and (4, 1). The triangle's sides are enlarged by a factor of 3 to form a new triangle. What is the area of the new triangle?
108 square units
54 square units
36 square units
None of the answers are correct
81 square units
54 square units
The points define a 3-4-5 right triangle. Its area is A = 1/2bh = ½(3)(4) = 6. The scale factor (SF) of the new triangle is 3. The area of the new triangle is given by Anew = (SF)2 x (Aold) =
32 x 6 = 9 x 6 = 54 square units (since the units are not given in the original problem).
NOTE: For a volume problem: Vnew = (SF)3 x (Vold).
Example Question #1 : How To Find If Right Triangles Are Similar
On a flat street, a light pole 36 feet tall casts a shadow that is 9 feet long. At the same time of day, a nearby light pole casts a shadow that is 6 feet long. How many feet tall is the second light pole?
Start by drawing out the light poles and their shadows.

In this case, we end up with two similar triangles. We know that these are similar triangles because the question tells us that these poles are on a flat surface, meaning angle B and angle E are both right angles. Then, because the question states that the shadow cast by both poles are at the same time of day, we know that angles C and F are equivalent. As a result, angles A and D must also be equivalent.
Since these are similar triangles, we can set up proportions for the corresponding sides.
Now, solve for 
Certified Tutor
All ACT Math Resources





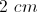





 ,
,  , and
, and  are collinear (they lie along the same line).
are collinear (they lie along the same line).  ,
,  ,
,  ,
, 
























