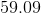We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

ACT Math : Triangles

Study concepts, example questions & explanations for ACT Math

Create An Account

All ACT Math Resources

14 Diagnostic Tests 767 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #171 : Act Math

Two similar triangles have perimeteres in the ratio 4:5 . The sides of the smaller triangle measure , , and respectively. What is the perimeter, in meters, of the larger triangle?

Possible Answers:

Correct answer:

Explanation:

Since the perimeter of the smaller triangle is 3m + 4m + 5m = 12m , and since the larger triangle has a perimeter in the 4:5 ratio, we can set up the following identity, where the perimeter of the larger triangle:

$\frac{12}{x} = \frac{4}5{}$

In cross multiplying this identity, we get 4x = 60 . We can now solve for . Here, x=15 , so the perimeter of the larger triangle is 15m .

Report an Error

Example Question #11 : Acute / Obtuse Triangles

_tri11

What is the value of in the triangle above? Round to the nearest hundredth.

Possible Answers:

100

71.31

91.41

59.09

Cannot be calculated

Correct answer:

59.09

Explanation:

Begin by filling in the missing angle for your triangle. Since a triangle has a total of 180 degrees, you know that the missing angle is:

180-50-30=100

Draw out the figure:

_tri12

Now, to solve this, you will need some trigonometry. Use the Law of Sines to calculate the value:

$\frac{sin(30)}{30}=\frac{sin(100)}{x}$

Solving for , you get:

$x=\frac{30sin(100)}{sin(30)}=59.0884651807326...$

Rounding, this is 59.09 .

Report an Error

Example Question #121 : Triangles

The base of a triangle is $8\ cm$ and the area is $48\ cm^2$ . The height of the triangle is then decreased by $75\%$ . What is the final area of the triangle?

Possible Answers:

$5\ cm$

$8\ cm$

$3\ cm$

$12\ cm$

$9\ cm$

Correct answer:

$12\ cm$

Explanation:

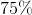
The formula for the area of a triangle is

$\frac{1}{2}b \times h$ .

If the area is equal to 48 cm² and the base is 8 cm, then the initial height is:

$48 = \frac{1}{2} \times 8 \times h$

h = 12

If 12 is decreased by 75% then

$12 \times .75 = 9$ , and 12 - 9 =3 . The final height is 3 cm.

Therefore the final area is

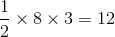
$\frac{1}{2}\times 8\times 3=12$ .

Report an Error

Example Question #11 : Acute / Obtuse Triangles

If the area of an isosceles triangle is and its base is , what is the height of the triangle?

Possible Answers:

Correct answer:

Explanation:

Use the formula for area of a triangle to solve for the height:

$A=\frac{1}{2}(b)(h)$

$50=\frac{1}{2}(10)(h)$

h=10

Report an Error

Example Question #2 : How To Find The Height Of An Acute / Obtuse Triangle

Find the height of the isosceles triangle above if the length of $\overline{AB}=12$ and $\overline{BC}=8$ . If your answer is in a decimal form, round to the nearest tenths place.

Possible Answers:

11.3

11.8

10.3

9.8

10.8

Correct answer:

11.3

Explanation:

Because this is an isosceles triangle, $\overline{AC}=\overline{AB}$ . Also, we know that the base of the triangle, $\overline{BC}=8$ . Therefore, we create two triangles by bisecting the trinagle down the center. We are solving for the length of the long arm of the triangle. We know that the hypotenuse is 12 and the base is 4 (half of 8).

Thus we use the Pythagorean Theorem to find the length of the long arm:

$12^{2} = 4^2+h^2$

$h = \sqrt{12^2-4^2}$

h=11.3

Report an Error

Example Question #14 : Acute / Obtuse Triangles

The triangle above has an area of units squared. If the length of the base is units, what is the height of the triangle?

Possible Answers:

1.5

4.5

Correct answer:

Explanation:

The area of a triangle is found using the formula

$A=\frac{1}{2}(base)(height)$

The height of any triangle is the length from it's highest point to the base, as pictured below:

We can find the height by rearranging the area formula:

$h = \frac{2A}{b} = \frac{2(15)}{10} = 3$

Report an Error

Example Question #354 : Plane Geometry

The ratio of the side lengths of a triangle is 7:10:11. In a similar triangle, the middle side is 9 inches long. What is the length of the longest side of the second triangle?

Possible Answers:

7.7

12.1

9.9

Correct answer:

9.9

Explanation:

Side lengths of similar triangles can be expressed in proportions. Establish a proportion comparing the middle and long sides of your triangles.

10/11 = 9/x

Cross multiply and solve for x.

10x = 99

x = 9.9

Report an Error

Example Question #355 : Plane Geometry

Two triangles are similar to each other. The bigger one has side lengths of 12, 3, and 14.

The smaller triangle's shortest side is 1 unit in length. What is the length of the smaller triangle's longest side?

Possible Answers:

$\frac{7}{6}$

$\frac{2}{3}$

$\frac{14}{3}$

Correct answer:

$\frac{14}{3}$

Explanation:

Because the triangles are similar, a ratio can be set up between the triangles' longest sides and shortest sides as such: 14/3 = x/1. Solving for x, we obtain that the shortest side of the triangle is 14/3 units long.

Report an Error

Example Question #122 : Triangles

The ratio of the side lengths of a triangle is 11:13:20 . The longest side of a similar triangle is . What is the length of the smallest side of that similar triangle?

Possible Answers:

12.9

13.2

14.3

11.7

Correct answer:

13.2

Explanation:

Use proportions to solve for the missing side:

$\frac{20}{24}=\frac{11}x{}$

Cross multiply and solve:

20x=(11)(24)

$\frac{264}{20}=x=13.2$

Report an Error

Example Question #12 : Acute / Obtuse Triangles

There are two similar triangles. One has side lengths of 14, 17, and 19. The smaller triangle's smallest side length is 2. What is the length of its longest side?

Possible Answers:

2.3

2.7

2.5

2.9

Correct answer:

2.7

Explanation:

Use proportions to solve for the missing side:

$\frac{2}{14}=\frac{x}{19}$

Cross multiply and solve:

(2)(19)=14x

$\frac{38}{14}=x=2.7$

Report an Error

View ACT Math Tutors

Soung
Certified Tutor

University of Chicago, Bachelor in Arts, Chemistry. Northwestern University, Doctor of Science, Molecular Pharmacology.

View ACT Math Tutors

Leonard
Certified Tutor

Florida State University, Bachelor of Science, Environmental Science.

View ACT Math Tutors

Madeline
Certified Tutor

University of Central Florida, Current Undergrad, Physics.

All ACT Math Resources

14 Diagnostic Tests 767 Practice Tests Question of the Day Flashcards Learn by Concept

ACT Math Tutors in Top Cities:

Atlanta ACT Math Tutors, Austin ACT Math Tutors, Boston ACT Math Tutors, Chicago ACT Math Tutors, Dallas Fort Worth ACT Math Tutors, Denver ACT Math Tutors, Houston ACT Math Tutors, Kansas City ACT Math Tutors, Los Angeles ACT Math Tutors, Miami ACT Math Tutors, New York City ACT Math Tutors, Philadelphia ACT Math Tutors, Phoenix ACT Math Tutors, San Diego ACT Math Tutors, San Francisco-Bay Area ACT Math Tutors, Seattle ACT Math Tutors, St. Louis ACT Math Tutors, Tucson ACT Math Tutors, Washington DC ACT Math Tutors

Popular Courses & Classes

Spanish Courses & Classes in Atlanta, SSAT Courses & Classes in Chicago, LSAT Courses & Classes in Chicago, LSAT Courses & Classes in Philadelphia, MCAT Courses & Classes in Seattle, LSAT Courses & Classes in Los Angeles, LSAT Courses & Classes in Boston, ISEE Courses & Classes in Washington DC, MCAT Courses & Classes in Miami, GRE Courses & Classes in San Francisco-Bay Area

Popular Test Prep

ISEE Test Prep in Los Angeles, SAT Test Prep in Denver, GMAT Test Prep in San Francisco-Bay Area, SSAT Test Prep in Dallas Fort Worth, GRE Test Prep in Philadelphia, LSAT Test Prep in Los Angeles, MCAT Test Prep in Seattle, SSAT Test Prep in Philadelphia, GRE Test Prep in New York City, ISEE Test Prep in New York City

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

ACT Math : Triangles

Study concepts, example questions & explanations for ACT Math

All ACT Math Resources

Example Questions

Example Question #171 : Act Math

Example Question #11 : Acute / Obtuse Triangles

Example Question #121 : Triangles

Example Question #11 : Acute / Obtuse Triangles

Example Question #2 : How To Find The Height Of An Acute / Obtuse Triangle

Example Question #14 : Acute / Obtuse Triangles

Example Question #354 : Plane Geometry

Example Question #355 : Plane Geometry

Example Question #122 : Triangles

Example Question #12 : Acute / Obtuse Triangles

All ACT Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: