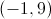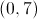The x intercept of an equation is the point at which it crosses the x-axis. To find the x intercept, plug in  for  and solve for .

To solve for , we can factor the equation. We must find two numbers that add to equal  and multiply to equal .  and  fit these conditions, giving:

We can set each of these equal to  to find two solutions for .

 and 

The x intercepts occur at these  values, giving the coordinates:

 and 

The x intercept of an equation is the point at which it crosses the x-axis. To find the x intercept, plug in  for  and solve for .

This equation is not easily factored, so to solve for , we can use the quadratic formula:

With the equation in the form

,

, , and .

Plugging these values into the quadratic formula, we get:

Find the two solutions for :

The x intercepts occur at these  values, giving the coordinates:

 and 

f(x) must be a parabola, since it contains an x² term. We are told that the vertex is below the x-axis, and that the focus is below the vertex. Because a parabola always opens toward the focus, f(x) must point downward. The general graph of the parabola must have a shape similar to this: 

Since the parabola points downward, the value of a must be less than zero. Also, since the parabola points downward, it must intersect the y-axis at a point below the origin; therefore, we know that the value of the y-coordinate of the y-intercept is less than zero. To find the y-coordinate of the y-intercept of f(x), we must find the value of f(x) where x = 0. (Any graph intersects the y-axis when x = 0.) When x = 0, f(0) = a(0) + b(0) + c = c. In other words, c represents the value of the y-intercept of f(x), which we have already established must be less than zero. To summarize, a and c must both be less than zero.

The last number we must analyze is b. One way to determine whether b must be negative is to assume that b is NOT negative, and see if f(x) still has a vertex below the x-axis and a focus below the vertex. In other words, let's pretend that b = 1 (we are told b is not zero), and see what happens. Because we know that a and c are negative, let's assume that a and c are both –1.

If b = 1, and if a and c = –1, then f(x) = –x² + x – 1. 

Let's graph f(x) by trying different values of x. 

If x = 0, f(x) = –1.

If x = 1, f(x) = –1. 

Because parabolas are symmetric, the vertex must have an x-value located halfway between 0 and 1. Thus, the x-value of the vertex is 1/2. To find the y-value of the vertex, we evaluate f(1/2).

f(1/2) = –(1/2)² + (1/2) – 1 = –1/4 + (1/2) – 1 = –3/4.

Thus, the vertex of f(x) would be located at (1/2, –3/4), which is below the x-axis. Also, because f(0) and f(1) are below the vertex, we know that the parabola opens downward, and the focus must be below the vertex.

To summarize, we have just provided an example in which b is greater than zero, where f(x) has a vertex below the x-axis and a focus below the vertex. In other words, it is possible for b > 0, so it is not true that b must be less than 0.  

Let's go back to the original question. We know that a and c are both less than zero, so we know choices I and III must be true; however, we have just shown that b doesn't necessarily have to be less than zero. In other words, only I and III (but not II) must be  true. 

The answer is I and III only.

Let's examine I, II, and III separately. 

Because the parabola points downward, the value of a must be less than zero. Thus, a < 0 must be true. 

Next, let's examine whether or not c < 0. The value of c is related to the y-intercept of f(x). If we let x = 0, then f(x) = f(0) = a(0) + b(0) + c = c. Thus, c is the value of the y-intercept of f(x). As we can see from the graph of f(x), the y-intercept is greater than 0. Therefore, c > 0. It is not possible for c < 0. This means choice II is incorrect. 

Lastly, we need to examine b² – 4ac, which is known as the discriminant of a quadratic equation. According to the quadratic formula, the roots of a quadratic equation are equal to the following: 

Notice, that in order for the values of x to be real, the value of b² – 4ac, which is under the square-root sign, must be greater than or equal to zero. If b² – 4ac is negative, then we are forced to take the square root of a negative number, which produces an imaginary (nonreal) result. Thus, it cannot be true that b² – 4ac < 0, and choice III cannot be correct.

Only choice I is correct.

The answer is I only. 

The -coordinate of the vertex is , where .

To get the -coordinate, evaluate .

The vertex is .

Because we are given the vertex of the parabola, the easiest way to solve this problem will involve the use of the formula of a parabola in vertex form. The vertex form of a parabola is given by the following equation:

f(x) = a(x – h)² + k, where (h, k) is the location of the vertex, and a is a constant.

Since the parabola has its vertex as (–3, 4), its equation in vertex form must be as follows:

f(x) = a(x – (–3)² + 4 = a(x + 3)² + 4

In order to complete the equation for the parabola, we must find the value of a. We can use the point (–1, –4), through which the parabola passes, in order to determine the value of a. We can substitute –1 in for x and –4 in for f(x).

f(x) = a(x + 3)² + 4

–4 = a(–1 + 3)² + 4

–4 = a(2)² + 4

–4 = 4a + 4

Subtract 4 from both sides.

–8 = 4a

Divide both sides by 4.

a = –2

This means that the final vertex form of the parabola is equal to f(x) = –2(x + 3)² + 4. However, since the answer choices are given in standard form, not vertex form, we must expand our equation for f(x) and write it in standard form.

f(x) = –2(x + 3)² + 4

= –2(x + 3)(x + 3) + 4

We can use the FOIL method to evaluate (x + 3)(x + 3).

= –2(x² + 3x + 3x + 9) + 4

= –2(x² + 6x + 9) + 4

= –2x² – 12x – 18 + 4

= –2x² – 12x – 14

The answer is f(x) = –2x² – 12x – 14.

Because the graph of f(x) = x² is symmetric about the y-axis, when we shift it downward, the points where it intersects the x-axis will be the same distance from the origin. In other words, we could say that one intercept will be (-a,0) and the other would be (a,0). The distance between these two points has to be 8, so that means that 2a = 8, and a = 4. This means that when f(x) is shifted downward, its new roots will be at (-4,0) and (4,0).

Let g(x) be the graph after f(x) has been shifted downward. We know that g(x) must have the roots (-4,0) and (4,0). We could thus write the equation of g(x) as (x-(-4))(x-4) = (x+4)(x-4) = x² - 16.

We can now compare f(x) and g(x), and we see that g(x) could be obtained if f(x) were shifted down by 16 units; therefore, the answer is 16.

The -intercept is , where :

The -intercept is .

The -intercept is :

 is the -intercept.

Since 4 can be raised to the power of any real number, the domain of  is the set of all real numbers. Therefore, there is no vertical asymptote of the graph of .