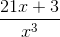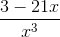ACT Math : Expressions
Study concepts, example questions & explanations for ACT Math
All ACT Math Resources
Example Questions
Example Question #1 : Expressions
Simplify the following rational expression: (9x - 2)/(x2) MINUS (6x - 8)/(x2)
Since both expressions have a common denominator, x2, we can just recopy the denominator and focus on the numerators. We get (9x - 2) - (6x - 8). We must distribute the negative sign over the 6x - 8 expression which gives us 9x - 2 - 6x + 8 ( -2 minus a -8 gives a +6 since a negative and negative make a positive). The numerator is therefore 3x + 6.
Example Question #3 : How To Add Rational Expressions With A Common Denominator
Simplify the following rational expression:
Since both fractions in the expression have a common denominator of 
Example Question #4 : How To Add Rational Expressions With A Common Denominator
Simplify the following expression:
Since both terms in the expression have the common denominator 
Example Question #5 : How To Add Rational Expressions With A Common Denominator
Simplify the following rational expression:
Since both rational terms in the expression have the common denominator 
Example Question #5 : How To Add Rational Expressions With A Common Denominator
Combine the following rational expressions:
When working with complex fractions, it is important not to let them intimidate you. They follow the same rules as regular fractions!
In this case, our problem is made easier by the fact that we already have a common denominator. Nothing fancy is required to start. Simply add the numerators:
For our next step, we need to combine like terms. This is easier to see if we group them together.
Thus, our final answer is:
Example Question #1 : How To Evaluate Algebraic Expressions
If x = y – 3, then (y – x)3 =
–27
3
–9
9
27
27
Solve for equation for y – x = 3. Then, plug in 3 into (y – x)3 = 27.
Example Question #1 : Evaluating Expressions
When graphed in the (x,y) coordinate plane, at what point do the lines -2x + 4y = 5 and y = -2 intersect?
(13/2,2)
(2,-2)
(13/2,-2)
(-13/2,-2)
(-13/2,-2)
Plugging in y=-2 in the second equation, gives x=-13/2. This is the point where the graphs intersect.
Example Question #31 : Expressions
The length in cm of a plastic container is 5cm less than triple its width. Which of the following equations is an accurate description of the length, l, as a function of the width, w?
l = 1/3w – 5
l = 3w – 5
l = 3w + 5
l = 5/3w + 3/5
l = 1/3w + 5
l = 3w – 5
This problem requires the development of an equation. We are told that the length is 5cm less than 3 times its width. So we should set up an equation that describes this situation. The equation l = 3w – 5 demonstrates how the length is 5 cm less than 3 times the width of the container.
Example Question #4 : How To Evaluate Algebraic Expressions
The expression x(9 + x)(x – 2) = 4 is a polynomial of which degree?
1
4
0
3
2
3
The highest power this polynomial can achieve is 3.
Example Question #1 : Evaluating Expressions
Given that x = 2 and y = 3, how much less is the value of 3x2 – 2y than the value of 3y2 – 2x?
17
29
47
1
6
17
First, we solve each expression by plugging in the given values for x and y:
3(22) – 2(3) = 12 – 6 = 6
3(32) – 2(2) = 27 – 4 = 23
Then we find the difference between the first and second expressions’ values:
23 – 6 = 17
Certified Tutor
Certified Tutor
All ACT Math Resources
